Sensing Method for Two-Target Detection in Time-Constrained Vector Poisson Channel
Paper and Code
Jan 19, 2022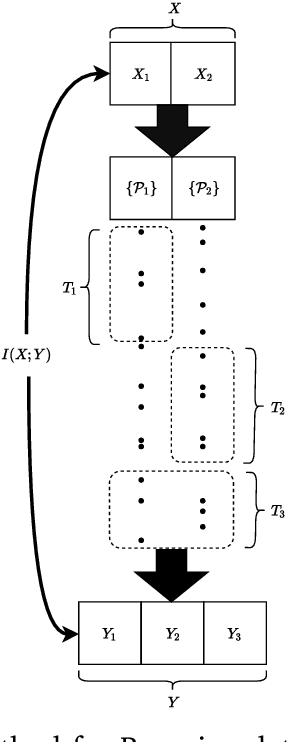
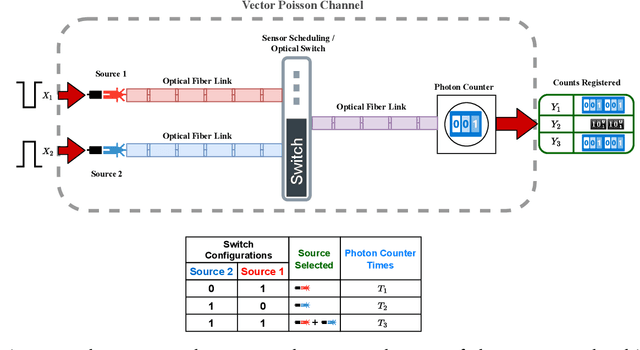
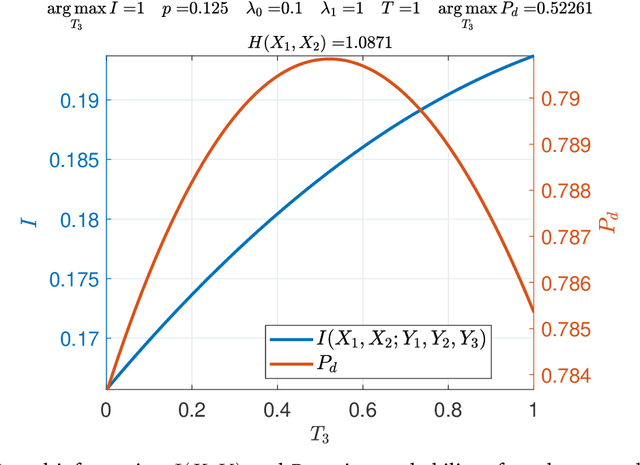
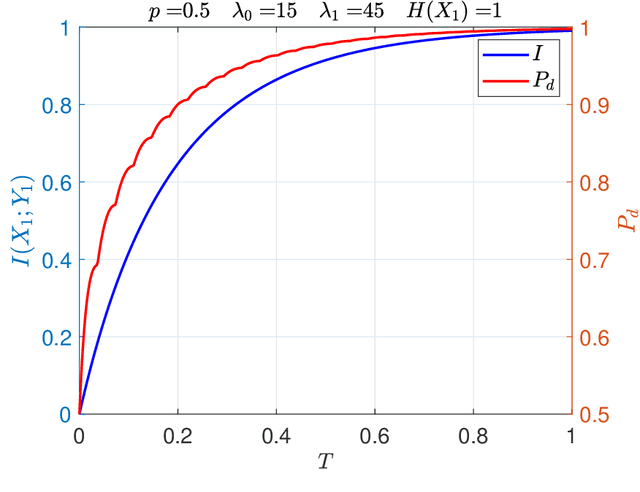
It is an experimental design problem in which there are two Poisson sources with two possible and known rates, and one counter. Through a switch, the counter can observe the sources individually or the counts can be combined so that the counter observes the sum of the two. The sensor scheduling problem is to determine an optimal proportion of the available time to be allocated toward individual and joint sensing, under a total time constraint. Two different metrics are used for optimization: mutual information between the sources and the observed counts, and probability of detection for the associated source detection problem. Our results, which are primarily computational, indicate similar but not identical results under the two cost functions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge