Craig Gotsman
A Scalable Heuristic for Fastest-Path Computation on Very Large Road Maps
Dec 18, 2018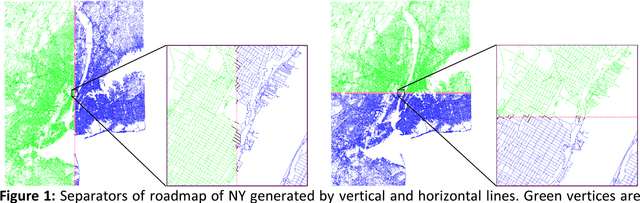
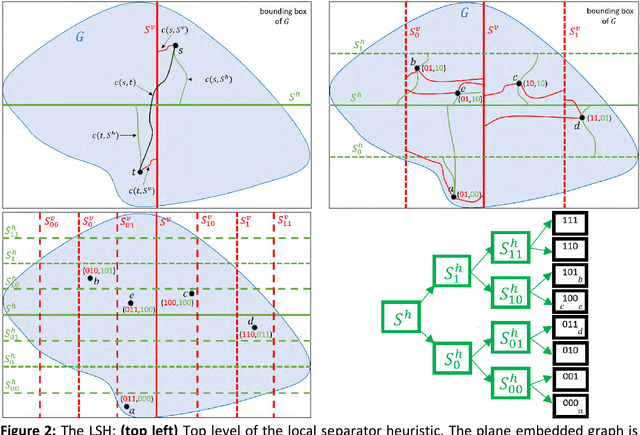
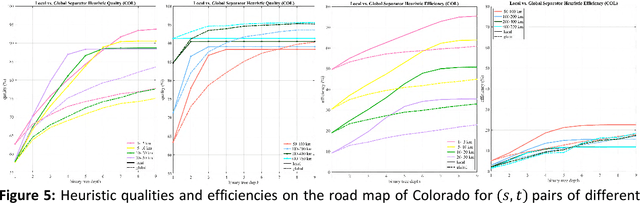
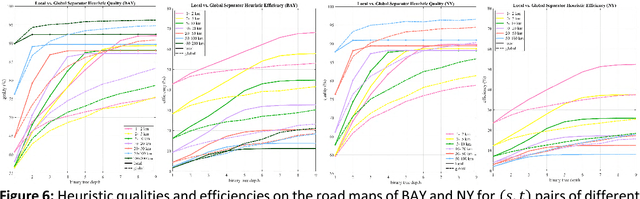
Abstract:Fastest-path queries between two points in a very large road map is an increasingly important primitive in modern transportation and navigation systems, thus very efficient computation of these paths is critical for system performance and throughput. We present a method to compute an effective heuristic for the fastest path travel time between two points on a road map, which can be used to significantly accelerate the classical A* algorithm when computing fastest paths. Our method is based on two hierarchical sets of separators of the map represented by two binary trees. A preprocessing step computes a short vector of values per road junction based on the separator trees, which is then stored with the map and used to efficiently compute the heuristic at the online query stage. We demonstrate experimentally that this method scales well to any map size, providing a better quality heuristic, thus more efficient A* search, for fastest path queries between points at all distances - especially small and medium range - relative to other known heuristics.
Efficient Fastest-Path Computations in Road Maps
Oct 02, 2018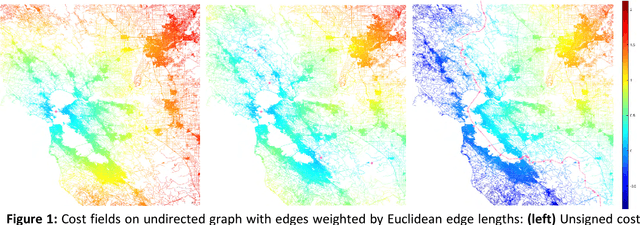


Abstract:In the age of real-time online traffic information and GPS-enabled devices, fastest-path computations between two points in a road network modeled as a directed graph, where each directed edge is weighted by a "travel time" value, are becoming a standard feature of many navigation-related applications. To support this, very efficient computation of these paths in very large road networks is critical. Fastest paths may be computed as minimal-cost paths in a weighted directed graph, but traditional minimal-cost path algorithms based on variants of the classic Dijkstra algorithm do not scale well, as in the worst case they may traverse the entire graph. A common improvement, which can dramatically reduce the number of traversed graph vertices, is the A* algorithm, which requires a good heuristic lower bound on the minimal cost. We introduce a simple, but very effective, heuristic function based on a small number of values assigned to each graph vertex. The values are based on graph separators and computed efficiently in a preprocessing stage. We present experimental results demonstrating that our heuristic provides estimates of the minimal cost which are superior to those of other heuristics. Our experiments show that when used in the A* algorithm, this heuristic can reduce the number of vertices traversed by an order of magnitude compared to other heuristics.
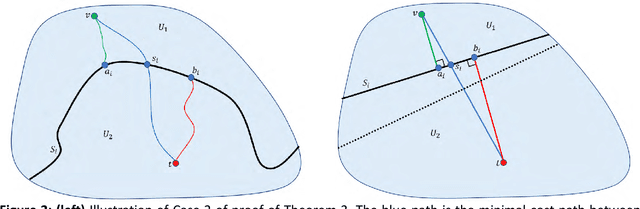
Practical Distance Functions for Path-Planning in Planar Domains
Aug 19, 2017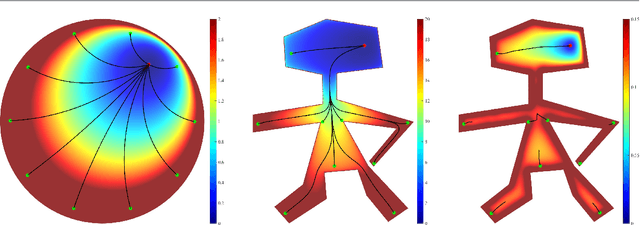
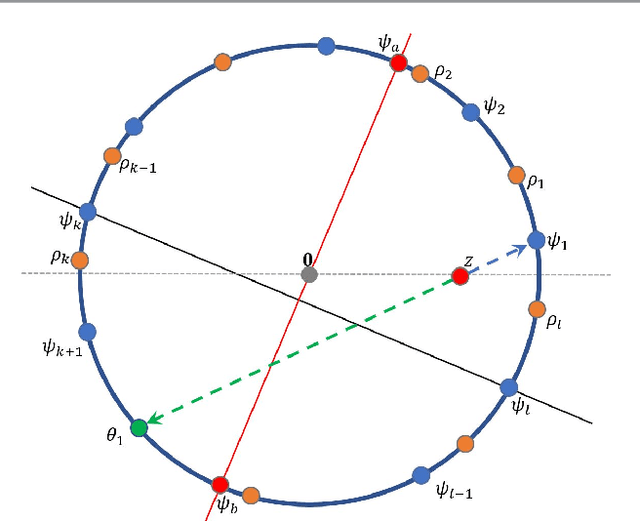
Abstract:Path planning is an important problem in robotics. One way to plan a path between two points $x,y$ within a (not necessarily simply-connected) planar domain $\Omega$, is to define a non-negative distance function $d(x,y)$ on $\Omega\times\Omega$ such that following the (descending) gradient of this distance function traces such a path. This presents two equally important challenges: A mathematical challenge -- to define $d$ such that $d(x,y)$ has a single minimum for any fixed $y$ (and this is when $x=y$), since a local minimum is in effect a "dead end", A computational challenge -- to define $d$ such that it may be computed efficiently. In this paper, given a description of $\Omega$, we show how to assign coordinates to each point of $\Omega$ and define a family of distance functions between points using these coordinates, such that both the mathematical and the computational challenges are met. This is done using the concepts of \emph{harmonic measure} and \emph{$f$-divergences}. In practice, path planning is done on a discrete network defined on a finite set of \emph{sites} sampled from $\Omega$, so any method that works well on the continuous domain must be adapted so that it still works well on the discrete domain. Given a set of sites sampled from $\Omega$, we show how to define a network connecting these sites such that a \emph{greedy routing} algorithm (which is the discrete equivalent of continuous gradient descent) based on the distance function mentioned above is guaranteed to generate a path in the network between any two such sites. In many cases, this network is close to a (desirable) planar graph, especially if the set of sites is dense.
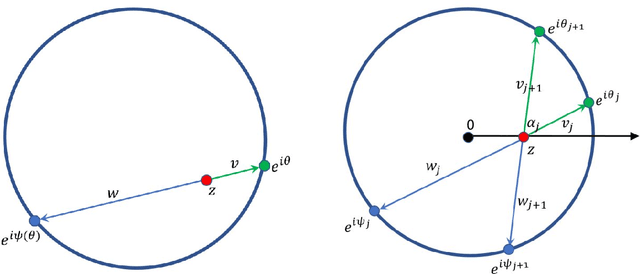
Path Planning with Divergence-Based Distance Functions
Aug 09, 2017



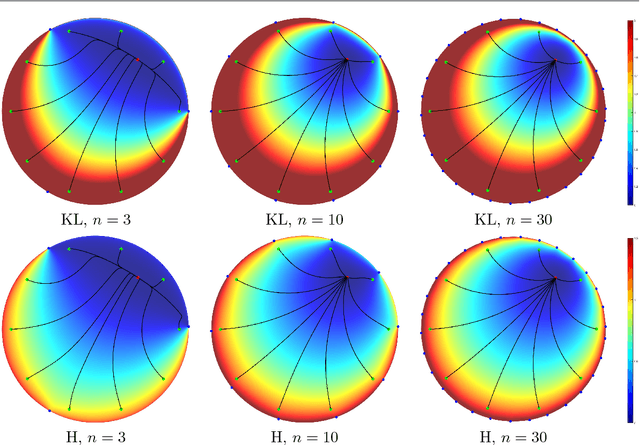
Abstract:Distance functions between points in a domain are sometimes used to automatically plan a gradient-descent path towards a given target point in the domain, avoiding obstacles that may be present. A key requirement from such distance functions is the absence of spurious local minima, which may foil such an approach, and this has led to the common use of harmonic potential functions. Based on the planar Laplace operator, the potential function guarantees the absence of spurious minima, but is well known to be slow to numerically compute and prone to numerical precision issues. To alleviate the first of these problems, we propose a family of novel divergence distances. These are based on f-divergence of the Poisson kernel of the domain. We define the divergence distances and compare them to the harmonic potential function and other related distance functions. Our first result is theoretical: We show that the family of divergence distances are equivalent to the harmonic potential function on simply-connected domains, namely generate paths which are identical to those generated by the potential function. The proof is based on the concept of conformal invariance. Our other results are more practical and relate to two special cases of divergence distances, one based on the Kullback-Leibler divergence and one based on the total variation divergence. We show that using divergence distances instead of the potential function and other distances has a significant computational advantage, as, following a pre-processing stage, they may be computed up to an order of magnitude faster than the others when taking advantage of certain sparsity properties of the Poisson kernel. Furthermore, the computation is "embarrassingly parallel", so may be implemented on a GPU with up to three orders of magnitude speedup.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge