Latent Channel Networks

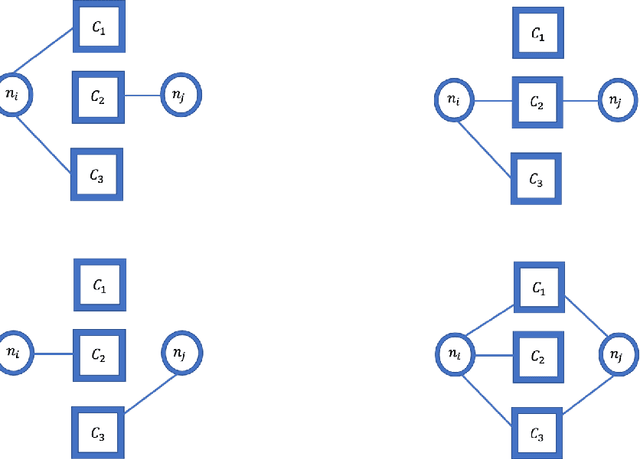
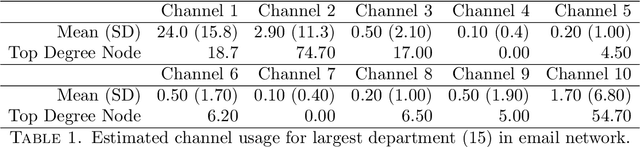
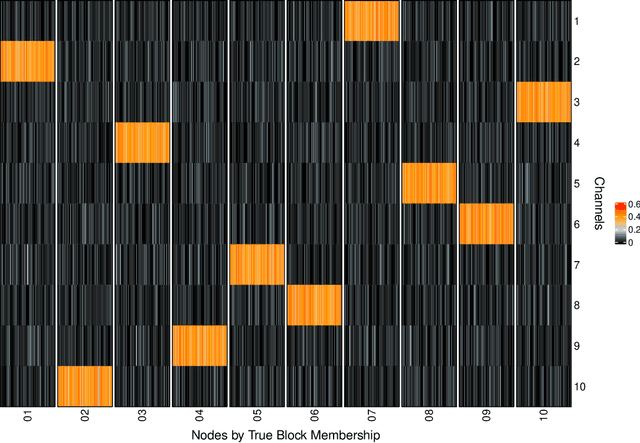
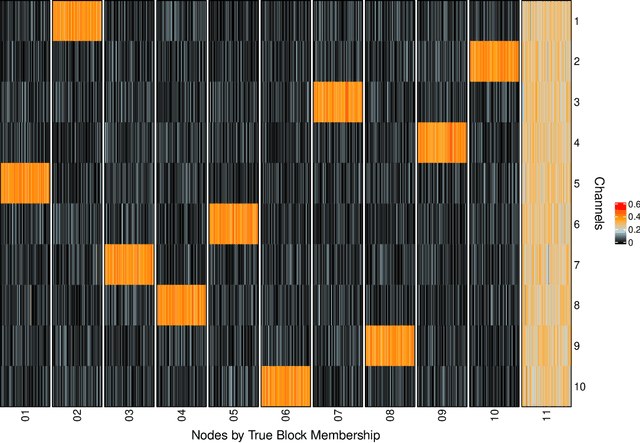
Latent Euclidean embedding models a given network by representing each node in a Euclidean space, where the probability of two nodes sharing an edge is a function of the distances between the nodes. This implies that for two nodes to share an edge with high probability, they must be relatively close in all dimensions. This constraint may be overly restrictive for describing modern networks, in which having similarities in at least one area may be sufficient for having a high edge probability. We introduce a new model, which we call Latent Channel Networks, which allows for such features of a network. We present an EM algorithm for fitting the model, for which the computational complexity is linear in the number of edges and number of channels and apply the algorithm to both synthetic and classic network datasets.

XPCA: Extending PCA for a Combination of Discrete and Continuous Variables

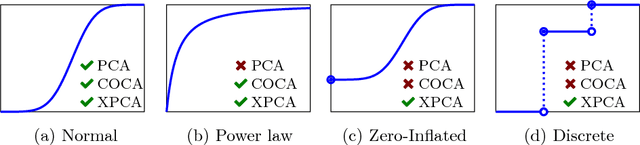
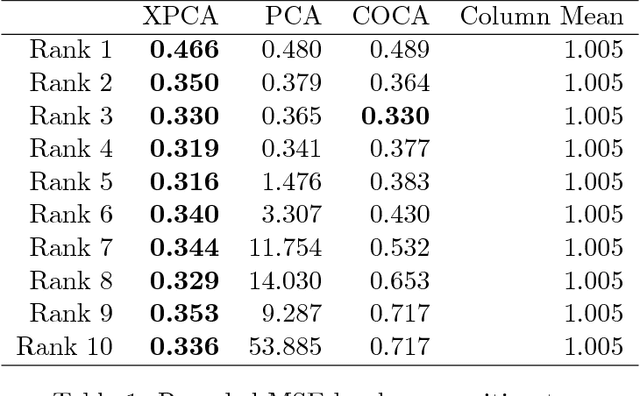
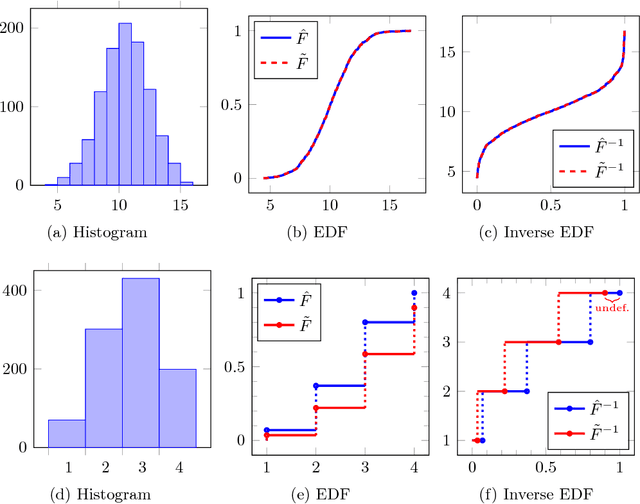
Principal component analysis (PCA) is arguably the most popular tool in multivariate exploratory data analysis. In this paper, we consider the question of how to handle heterogeneous variables that include continuous, binary, and ordinal. In the probabilistic interpretation of low-rank PCA, the data has a normal multivariate distribution and, therefore, normal marginal distributions for each column. If some marginals are continuous but not normal, the semiparametric copula-based principal component analysis (COCA) method is an alternative to PCA that combines a Gaussian copula with nonparametric marginals. If some marginals are discrete or semi-continuous, we propose a new extended PCA (XPCA) method that also uses a Gaussian copula and nonparametric marginals and accounts for discrete variables in the likelihood calculation by integrating over appropriate intervals. Like PCA, the factors produced by XPCA can be used to find latent structure in data, build predictive models, and perform dimensionality reduction. We present the new model, its induced likelihood function, and a fitting algorithm which can be applied in the presence of missing data. We demonstrate how to use XPCA to produce an estimated full conditional distribution for each data point, and use this to produce to provide estimates for missing data that are automatically range respecting. We compare the methods as applied to simulated and real-world data sets that have a mixture of discrete and continuous variables.