Latent Channel Networks
Paper and Code
Jun 10, 2019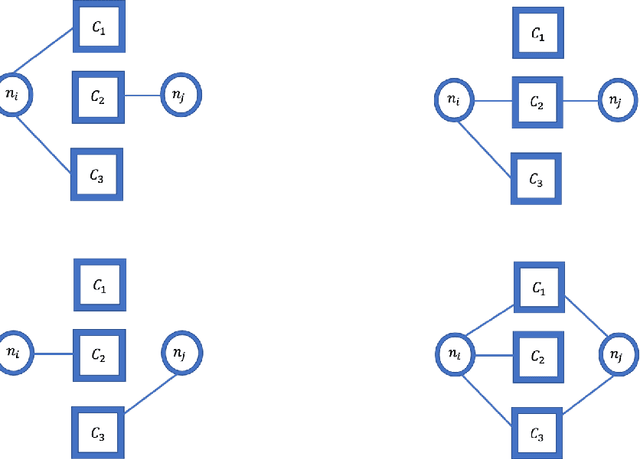
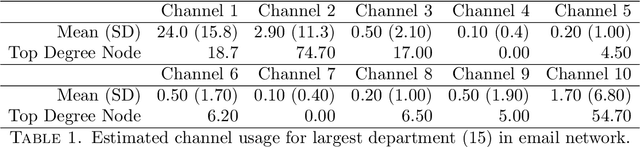
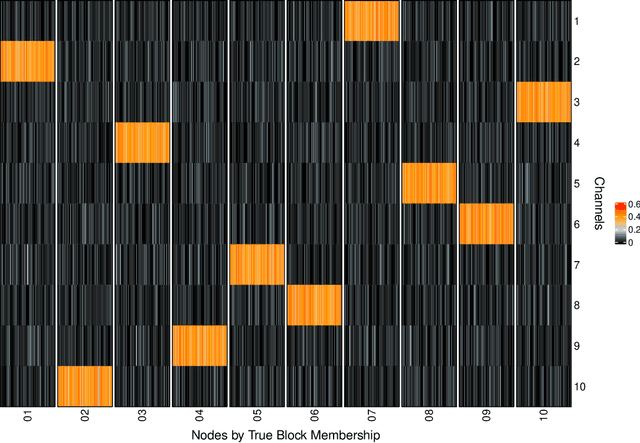
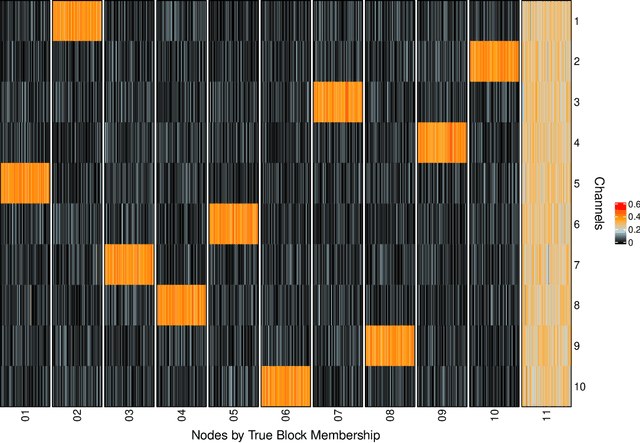
Latent Euclidean embedding models a given network by representing each node in a Euclidean space, where the probability of two nodes sharing an edge is a function of the distances between the nodes. This implies that for two nodes to share an edge with high probability, they must be relatively close in all dimensions. This constraint may be overly restrictive for describing modern networks, in which having similarities in at least one area may be sufficient for having a high edge probability. We introduce a new model, which we call Latent Channel Networks, which allows for such features of a network. We present an EM algorithm for fitting the model, for which the computational complexity is linear in the number of edges and number of channels and apply the algorithm to both synthetic and classic network datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge