Joint Power Allocation and Reflecting-Element Activation for Energy Efficiency Maximization in IRS-Aided Communications Under CSI Uncertainty

We study the joint power allocation and reflecting element (RE) activation to maximize the energy efficiency (EE) in communication systems assisted by an intelligent reflecting surface (IRS), taking into account imperfections in channel state information (CSI). The robust optimization problem is mixed integer, i.e., the optimization variables are continuous (transmit power) and discrete (binary states of REs). In order to solve this challenging problem we develop two algorithms. The first one is an alternating optimization (AO) method that attains a suboptimal solution with low complexity, based on the Lambert W function and a dynamic programming (DP) algorithm. The second one is a branch-and-bound (B&B) method that uses AO as its subroutine and is formally guaranteed to achieve a globally optimal solution. Both algorithms do not require any external optimization solver for their implementation. Furthermore, numerical results show that the proposed algorithms outperform the baseline schemes, AO achieves near-optimal performance in most cases, and B&B has low computational complexity on average.

Transmit and Receive Antenna Port Selection for Channel Capacity Maximization in Fluid-MIMO Systems

In this letter, we study a discrete optimization problem, namely, the maximization of channel capacity in fluid multiple-input multiple-output (fluid-MIMO) systems through the selection of antenna ports/positions at the transmitter and the receiver. First, we present a new joint convex relaxation (JCR) problem by using an upper bound on the channel capacity and exploiting the binary nature of optimization variables. Then, we develop and analyze two optimization algorithms with different performance-complexity tradeoffs: the first is based on JCR and reduced exhaustive search (JCR&RES), while the second on JCR and alternating optimization (JCR&AO). Finally, numerical results show that the proposed algorithms significantly outperform two baseline schemes, the random port selection and the conventional MIMO setup.

Robust IRS-Element Activation for Energy Efficiency Optimization in IRS-Assisted Communication Systems With Imperfect CSI

In this paper, we study an intelligent reflecting surface (IRS)-aided communication system with single-antenna transmitter and receiver, under imperfect channel state information (CSI). More specifically, we deal with the robust selection of binary (on/off) states of the IRS elements in order to maximize the worst-case energy efficiency (EE), given a bounded CSI uncertainty, while satisfying a minimum signal-to-noise ratio (SNR). In addition, we consider not only continuous but also discrete IRS phase shifts. First, we derive closed-form expressions of the worst-case SNRs, and then formulate the robust (discrete) optimization problems for each case. In the case of continuous phase shifts, we design a dynamic programming (DP) algorithm that is theoretically guaranteed to achieve the global maximum with polynomial complexity $O(L\,{\log L})$, where $L$ is the number of IRS elements. In the case of discrete phase shifts, we develop a convex-relaxation-based method (CRBM) to obtain a feasible (sub-optimal) solution in polynomial time $O(L^{3.5})$, with a posteriori performance guarantee. Furthermore, numerical simulations provide useful insights and confirm the theoretical results. In particular, the proposed algorithms are several orders of magnitude faster than the exhaustive search when $L$ is large, thus being highly scalable and suitable for practical applications. Moreover, both algorithms outperform a baseline scheme, namely, the activation of all IRS elements.

Global Optimization of Energy Efficiency in IRS-Aided Communication Systems via Robust IRS-Element Activation

In this paper, we study an intelligent reflecting surface (IRS) assisted communication system with single-antenna transmitter and receiver, under imperfect channel state information (CSI). More specifically, we deal with the robust selection of binary (on/off) states of the IRS elements in order to maximize the worst-case energy efficiency (EE), given a bounded CSI uncertainty, while satisfying a minimum signal-to-noise ratio (SNR). The IRS phase shifts are adjusted so as to maximize the ideal SNR (i.e., without CSI error), based only on the estimated channels. First, we derive a closed-form expression of the worst-case SNR, and then formulate the robust (discrete) optimization problem. Moreover, we design and analyze a dynamic programming (DP) algorithm that is theoretically guaranteed to achieve the global maximum with polynomial complexity $O(L \log L)$, where $L$ is the number of IRS elements. Finally, numerical simulations confirm the theoretical results. In particular, the proposed algorithm shows identical performance with the exhaustive search, and significantly outperforms a baseline scheme, namely, the activation of all IRS elements.

Joint IRS Location and Size Optimization in Multi-IRS Aided Two-Way Full-Duplex Communication Systems

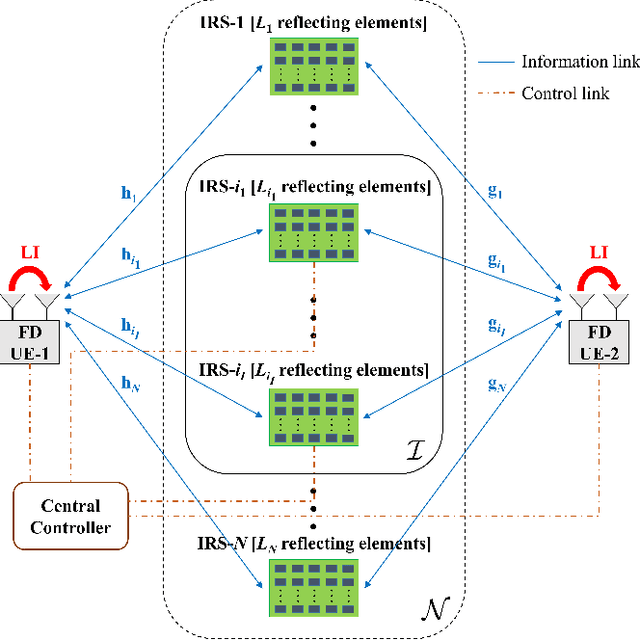
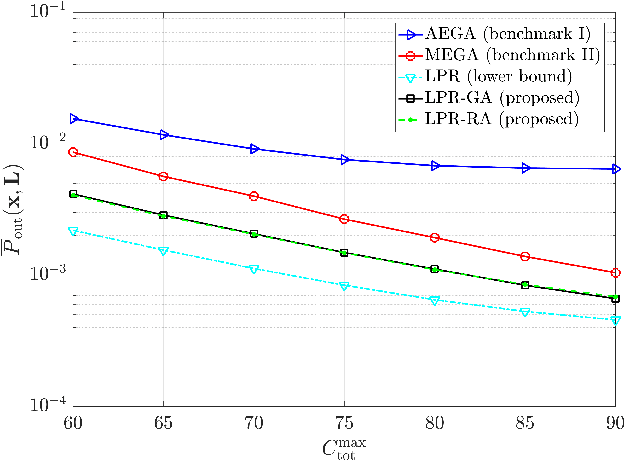
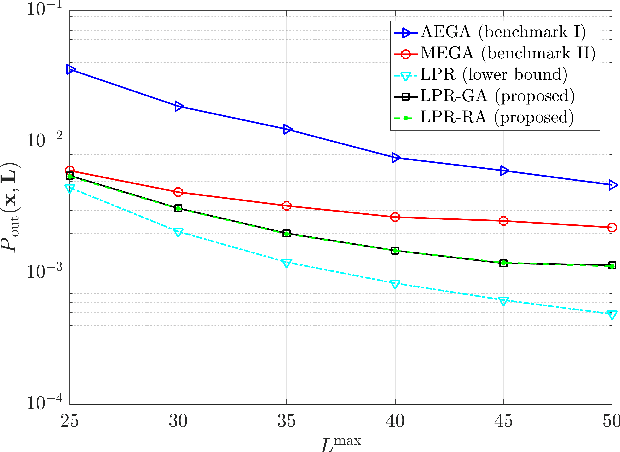
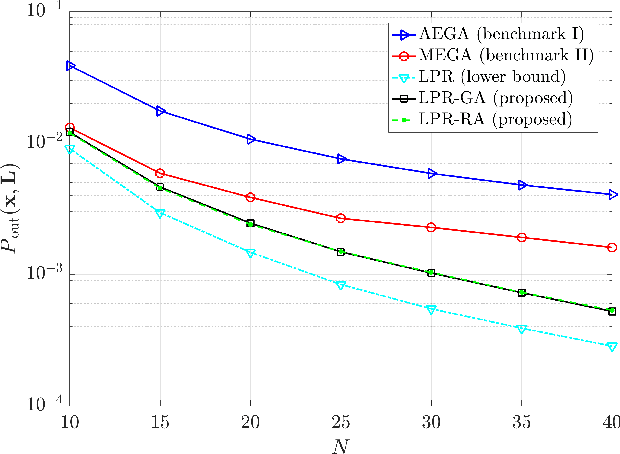
Intelligent reflecting surfaces (IRSs) have emerged as a promising wireless technology for the dynamic configuration and control of electromagnetic waves, thus creating a smart (programmable) radio environment. In this context, we study a multi-IRS assisted two-way communication system consisting of two users that employ full-duplex (FD) technology. More specifically, we deal with the joint IRS location and size (i.e., the number of reflecting elements) optimization in order to minimize an upper bound of system outage probability under various constraints, namely, minimum and maximum number of reflecting elements per IRS, maximum number of installed IRSs, maximum total number of reflecting elements (implicit bound on the signaling overhead) as well as maximum total IRS installation cost. First, the problem is formulated as a discrete optimization problem and, then, a theoretical proof of its NP-hardness is given. Moreover, we provide a lower bound on the optimum value by solving a linear-programming relaxation (LPR) problem. Subsequently, we design two polynomial-time algorithms, a deterministic greedy algorithm and a randomized approximation algorithm, based on the LPR solution. The former is a heuristic method that always computes a feasible solution for which (a posteriori) performance guarantee can be provided. The latter achieves an approximate solution, using randomized rounding, with provable (a priori) probabilistic guarantees on the performance. Furthermore, extensive numerical simulations demonstrate the superiority of the proposed algorithms compared to the baseline schemes. Finally, useful conclusions regarding the comparison between FD and conventional half-duplex (HD) systems are also drawn.