Joint IRS Location and Size Optimization in Multi-IRS Aided Two-Way Full-Duplex Communication Systems

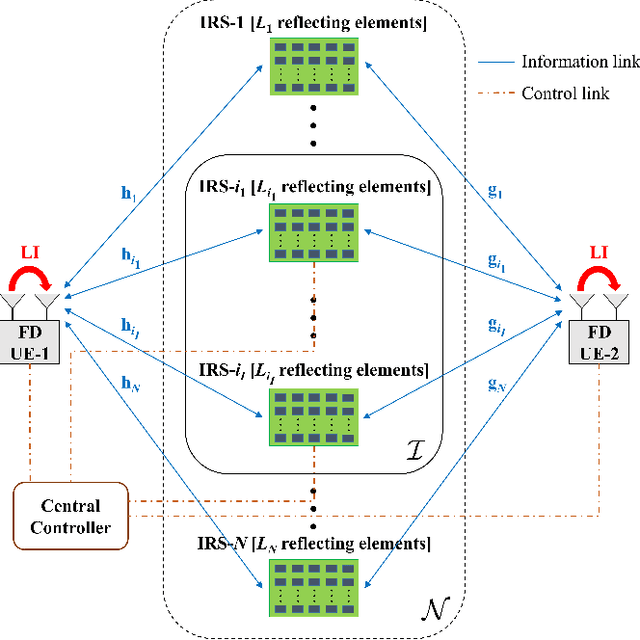
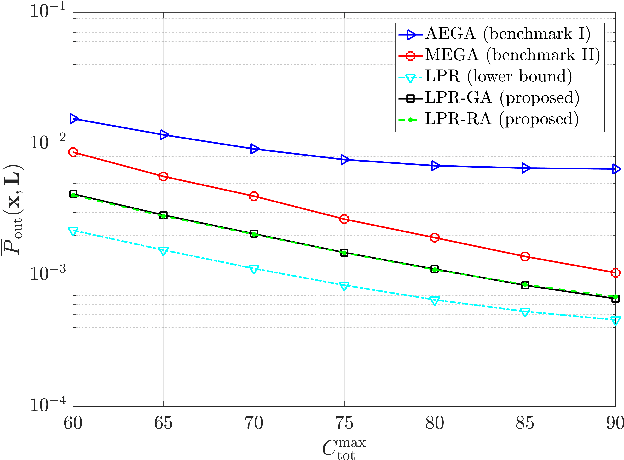
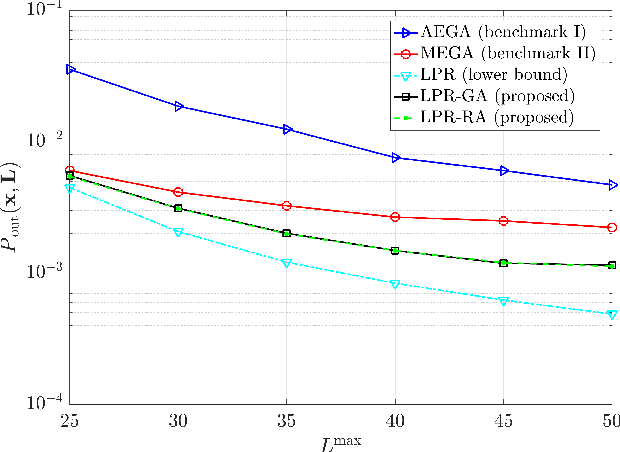
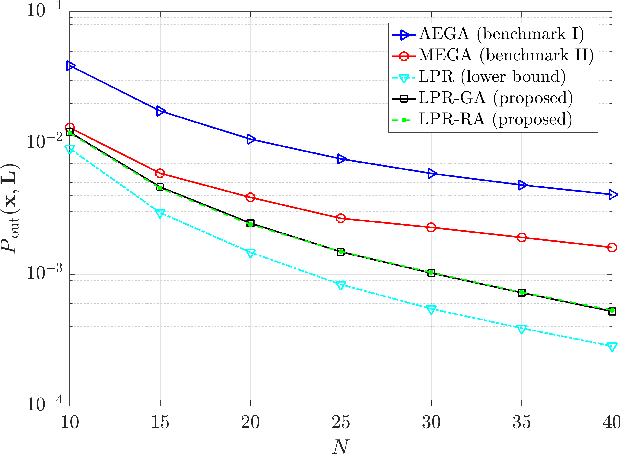
Intelligent reflecting surfaces (IRSs) have emerged as a promising wireless technology for the dynamic configuration and control of electromagnetic waves, thus creating a smart (programmable) radio environment. In this context, we study a multi-IRS assisted two-way communication system consisting of two users that employ full-duplex (FD) technology. More specifically, we deal with the joint IRS location and size (i.e., the number of reflecting elements) optimization in order to minimize an upper bound of system outage probability under various constraints, namely, minimum and maximum number of reflecting elements per IRS, maximum number of installed IRSs, maximum total number of reflecting elements (implicit bound on the signaling overhead) as well as maximum total IRS installation cost. First, the problem is formulated as a discrete optimization problem and, then, a theoretical proof of its NP-hardness is given. Moreover, we provide a lower bound on the optimum value by solving a linear-programming relaxation (LPR) problem. Subsequently, we design two polynomial-time algorithms, a deterministic greedy algorithm and a randomized approximation algorithm, based on the LPR solution. The former is a heuristic method that always computes a feasible solution for which (a posteriori) performance guarantee can be provided. The latter achieves an approximate solution, using randomized rounding, with provable (a priori) probabilistic guarantees on the performance. Furthermore, extensive numerical simulations demonstrate the superiority of the proposed algorithms compared to the baseline schemes. Finally, useful conclusions regarding the comparison between FD and conventional half-duplex (HD) systems are also drawn.