Applications of Online Nonnegative Matrix Factorization to Image and Time-Series Data

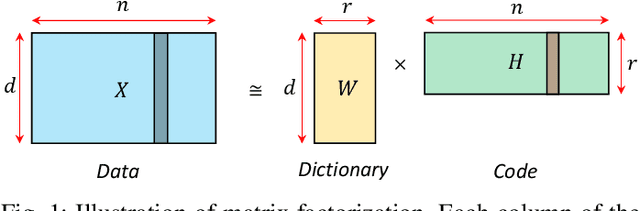
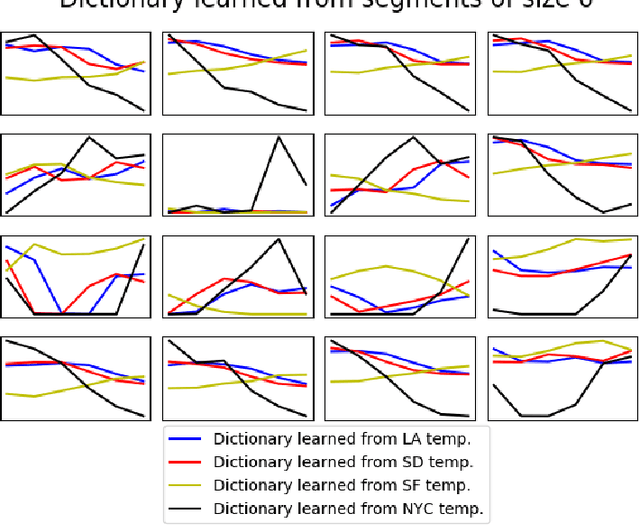
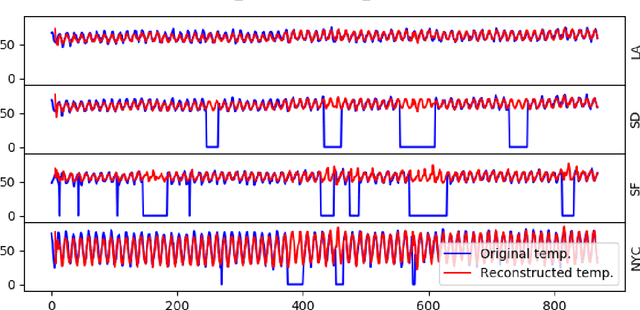
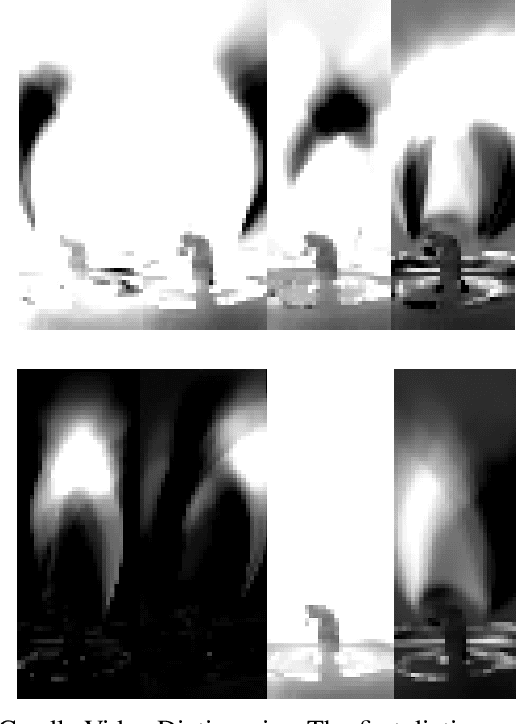
Online nonnegative matrix factorization (ONMF) is a matrix factorization technique in the online setting where data are acquired in a streaming fashion and the matrix factors are updated each time. This enables factor analysis to be performed concurrently with the arrival of new data samples. In this article, we demonstrate how one can use online nonnegative matrix factorization algorithms to learn joint dictionary atoms from an ensemble of correlated data sets. We propose a temporal dictionary learning scheme for time-series data sets, based on ONMF algorithms. We demonstrate our dictionary learning technique in the application contexts of historical temperature data, video frames, and color images.

Online nonnegative tensor factorization and CP-dictionary learning for Markovian data

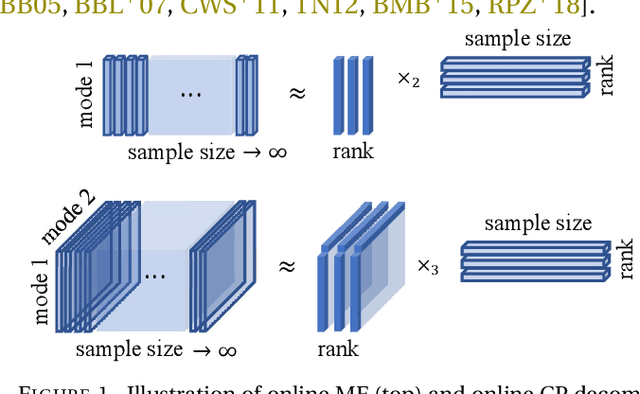
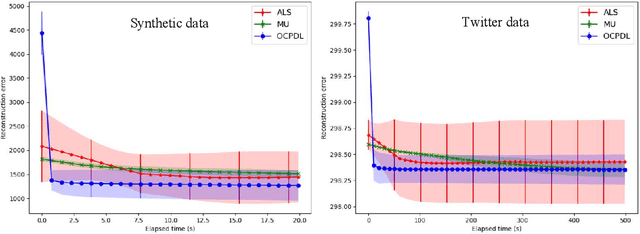
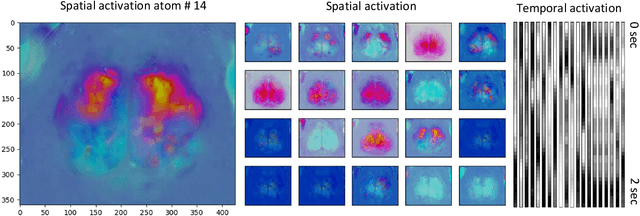
Nonnegative Matrix Factorization (NMF) algorithms are fundamental tools in learning low-dimensional features from vector-valued data, Nonnegative Tensor Factorization (NTF) algorithms serve a similar role for dictionary learning problems for multi-modal data. Also, there is often a critical interest in \textit{online} versions of such factorization algorithms to learn progressively from minibatches, without requiring the full data as in conventional algorithms. However, the current theory of Online NTF algorithms is quite nascent, especially compared to the comprehensive literature on online NMF algorithms. In this work, we introduce a novel online NTF algorithm that learns a CP basis from a given stream of tensor-valued data under general constraints. In particular, using nonnegativity constraints, the learned CP modes also give localized dictionary atoms that respect the tensor structure in multi-model data. On the application side, we demonstrate the utility of our algorithm on a diverse set of examples from image, video, and time series data, illustrating how one may learn qualitatively different CP-dictionaries by not needing to reshape tensor data before the learning process. On the theoretical side, we prove that our algorithm converges to the set of stationary points of the objective function under the hypothesis that the sequence of data tensors have functional Markovian dependence. This assumption covers a wide range of application contexts including data streams generated by independent or MCMC sampling.

COVID-19 Time-series Prediction by Joint Dictionary Learning and Online NMF

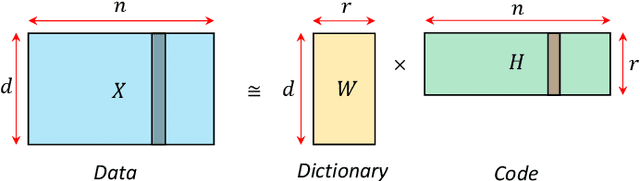
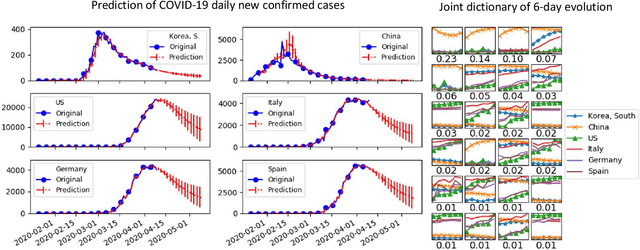
Predicting the spread and containment of COVID-19 is a challenge of utmost importance that the broader scientific community is currently facing. One of the main sources of difficulty is that a very limited amount of daily COVID-19 case data is available, and with few exceptions, the majority of countries are currently in the "exponential spread stage," and thus there is scarce information available which would enable one to predict the phase transition between spread and containment. In this paper, we propose a novel approach to predicting the spread of COVID-19 based on dictionary learning and online nonnegative matrix factorization (online NMF). The key idea is to learn dictionary patterns of short evolution instances of the new daily cases in multiple countries at the same time, so that their latent correlation structures are captured in the dictionary patterns. We first learn such patterns by minibatch learning from the entire time-series and then further adapt them to the time-series by online NMF. As we progressively adapt and improve the learned dictionary patterns to the more recent observations, we also use them to make one-step predictions by the partial fitting. Lastly, by recursively applying the one-step predictions, we can extrapolate our predictions into the near future. Our prediction results can be directly attributed to the learned dictionary patterns due to their interpretability.