Reinforcement Learning for Physical Layer Communications

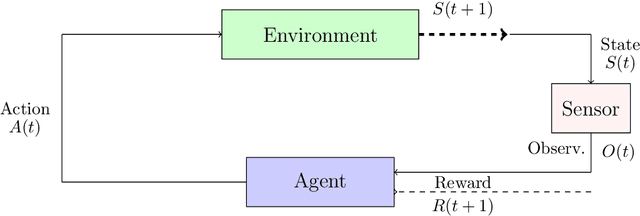
In this chapter, we will give comprehensive examples of applying RL in optimizing the physical layer of wireless communications by defining different class of problems and the possible solutions to handle them. In Section 9.2, we present all the basic theory needed to address a RL problem, i.e. Markov decision process (MDP), Partially observable Markov decision process (POMDP), but also two very important and widely used algorithms for RL, i.e. the Q-learning and SARSA algorithms. We also introduce the deep reinforcement learning (DRL) paradigm and the section ends with an introduction to the multi-armed bandits (MAB) framework. Section 9.3 focuses on some toy examples to illustrate how the basic concepts of RL are employed in communication systems. We present applications extracted from literature with simplified system models using similar notation as in Section 9.2 of this Chapter. In Section 9.3, we also focus on modeling RL problems, i.e. how action and state spaces and rewards are chosen. The Chapter is concluded in Section 9.4 with a prospective thought on RL trends and it ends with a review of a broader state of the art in Section 9.5.

Collaboration and Coordination in Secondary Networks for Opportunistic Spectrum Access

In this paper, we address the general case of a coordinated secondary network willing to exploit communication opportunities left vacant by a licensed primary network. Since secondary users (SU) usually have no prior knowledge on the environment, they need to learn the availability of each channel through sensing techniques, which however can be prone to detection errors. We argue that cooperation among secondary users can enable efficient learning and coordination mechanisms in order to maximize the spectrum exploitation by SUs, while minimizing the impact on the primary network. To this goal, we provide three novel contributions in this paper. First, we formulate the spectrum selection in secondary networks as an instance of the Multi-Armed Bandit (MAB) problem, and we extend the analysis to the collaboration learning case, in which each SU learns the spectrum occupation, and shares this information with other SUs. We show that collaboration among SUs can mitigate the impact of sensing errors on system performance, and improve the convergence of the learning process to the optimal solution. Second, we integrate the learning algorithms with two collaboration techniques based on modified versions of the Hungarian algorithm and of the Round Robin algorithm that allows reducing the interference among SUs. Third, we derive fundamental limits to the performance of cooperative learning algorithms based on Upper Confidence Bound (UCB) policies in a symmetric scenario where all SU have the same perception of the quality of the resources. Extensive simulation results confirm the effectiveness of our joint learning-collaboration algorithm in protecting the operations of Primary Users (PUs), while maximizing the performance of SUs.

UCB Algorithm for Exponential Distributions

We introduce in this paper a new algorithm for Multi-Armed Bandit (MAB) problems. A machine learning paradigm popular within Cognitive Network related topics (e.g., Spectrum Sensing and Allocation). We focus on the case where the rewards are exponentially distributed, which is common when dealing with Rayleigh fading channels. This strategy, named Multiplicative Upper Confidence Bound (MUCB), associates a utility index to every available arm, and then selects the arm with the highest index. For every arm, the associated index is equal to the product of a multiplicative factor by the sample mean of the rewards collected by this arm. We show that the MUCB policy has a low complexity and is order optimal.