Progressive Focus Search for the Static and Stochastic VRPTW with both Random Customers and Reveal Times

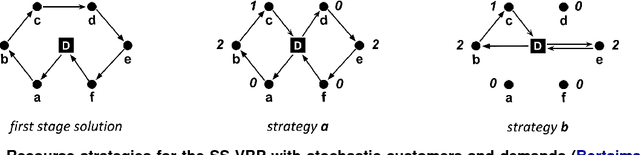
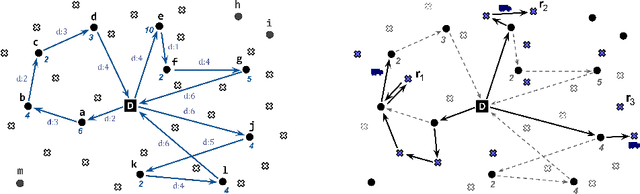
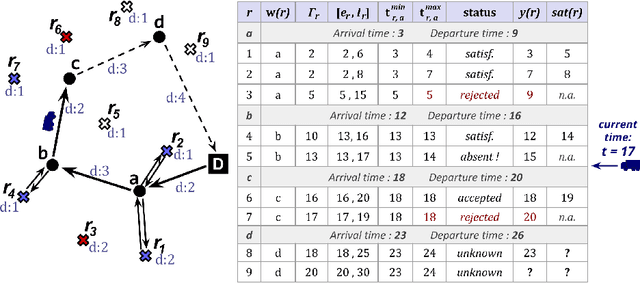
Static stochastic VRPs aim at modeling real-life VRPs by considering uncertainty on data. In particular, the SS-VRPTW-CR considers stochastic customers with time windows and does not make any assumption on their reveal times, which are stochastic as well. Based on customer request probabilities, we look for an a priori solution composed preventive vehicle routes, minimizing the expected number of unsatisfied customer requests at the end of the day. A route describes a sequence of strategic vehicle relocations, from which nearby requests can be rapidly reached. Instead of reoptimizing online, a so-called recourse strategy defines the way the requests are handled, whenever they appear. In this paper, we describe a new recourse strategy for the SS-VRPTW-CR, improving vehicle routes by skipping useless parts. We show how to compute the expected cost of a priori solutions, in pseudo-polynomial time, for this recourse strategy. We introduce a new meta-heuristic, called Progressive Focus Search (PFS), which may be combined with any local-search based algorithm for solving static stochastic optimization problems. PFS accelerates the search by using approximation factors: from an initial rough simplified problem, the search progressively focuses to the actual problem description. We evaluate our contributions on a new, real-world based, public benchmark.

The Static and Stochastic VRPTW with both random Customers and Reveal Times: algorithms and recourse strategies

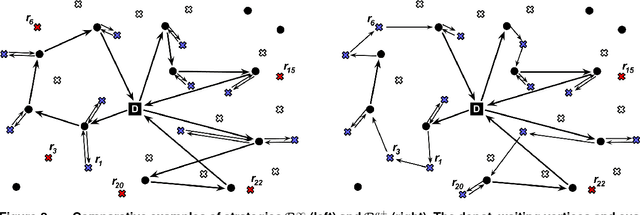
Unlike its deterministic counterpart, static and stochastic vehicle routing problems (SS-VRP) aim at modeling and solving real-life operational problems by considering uncertainty on data. We consider the SS-VRPTW-CR introduced in Saint-Guillain et al. (2017). Like the SS-VRP introduced by Bertsimas (1992), we search for optimal first stage routes for a fleet of vehicles to handle a set of stochastic customer demands, i.e., demands are uncertain and we only know their probabilities. In addition to capacity constraints, customer demands are also constrained by time windows. Unlike all SS-VRP variants, the SS-VRPTW-CR does not make any assumption on the time at which a stochastic demand is revealed, i.e., the reveal time is stochastic as well. To handle this new problem, we introduce waiting locations: Each vehicle is assigned a sequence of waiting locations from which it may serve some associated demands, and the objective is to minimize the expected number of demands that cannot be satisfied in time. In this paper, we propose two new recourse strategies for the SS-VRPTW-CR, together with their closed-form expressions for efficiently computing their expectations: The first one allows us to take vehicle capacities into account; The second one allows us to optimize routes by avoiding some useless trips. We propose two algorithms for searching for routes with optimal expected costs: The first one is an extended branch-and-cut algorithm, based on a stochastic integer formulation, and the second one is a local search based heuristic method. We also introduce a new public benchmark for the SS-VRPTW-CR, based on real-world data coming from the city of Lyon. We evaluate our two algorithms on this benchmark and empirically demonstrate the expected superiority of the SS-VRPTW-CR anticipative actions over a basic "wait-and-serve" policy.

A Multistage Stochastic Programming Approach to the Dynamic and Stochastic VRPTW - Extended version

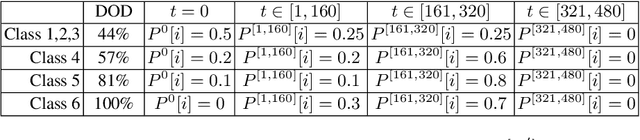
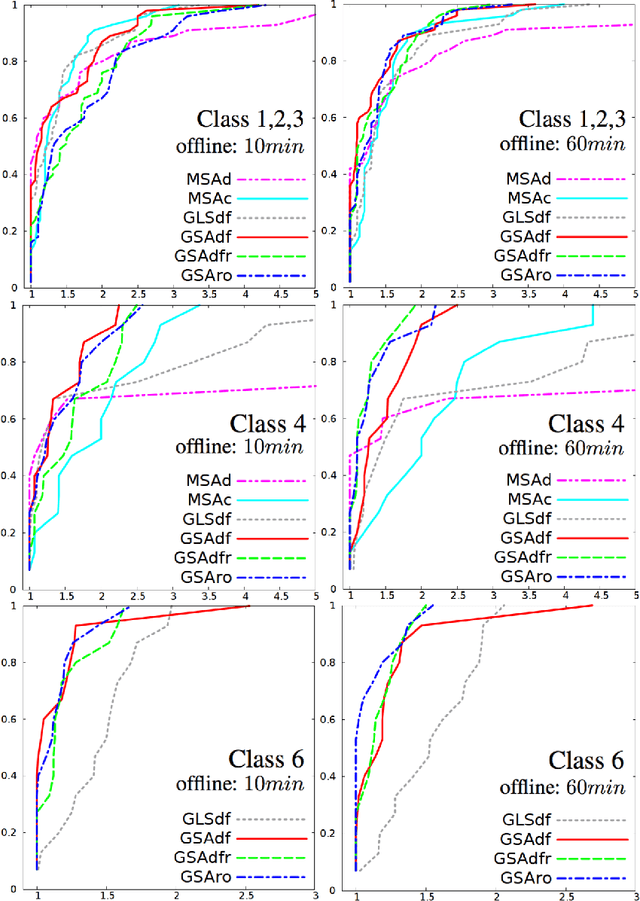
We consider a dynamic vehicle routing problem with time windows and stochastic customers (DS-VRPTW), such that customers may request for services as vehicles have already started their tours. To solve this problem, the goal is to provide a decision rule for choosing, at each time step, the next action to perform in light of known requests and probabilistic knowledge on requests likelihood. We introduce a new decision rule, called Global Stochastic Assessment (GSA) rule for the DS-VRPTW, and we compare it with existing decision rules, such as MSA. In particular, we show that GSA fully integrates nonanticipativity constraints so that it leads to better decisions in our stochastic context. We describe a new heuristic approach for efficiently approximating our GSA rule. We introduce a new waiting strategy. Experiments on dynamic and stochastic benchmarks, which include instances of different degrees of dynamism, show that not only our approach is competitive with state-of-the-art methods, but also enables to compute meaningful offline solutions to fully dynamic problems where absolutely no a priori customer request is provided.

Proceedings 6th International Workshop on Local Search Techniques in Constraint Satisfaction

LSCS is a satellite workshop of the international conference on principles and practice of Constraint Programming (CP), since 2004. It is devoted to local search techniques in constraint satisfaction, and focuses on all aspects of local search techniques, including: design and implementation of new algorithms, hybrid stochastic-systematic search, reactive search optimization, adaptive search, modeling for local-search, global constraints, flexibility and robustness, learning methods, and specific applications.