A Multistage Stochastic Programming Approach to the Dynamic and Stochastic VRPTW - Extended version
Paper and Code
Feb 06, 2015
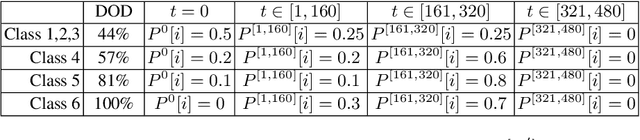
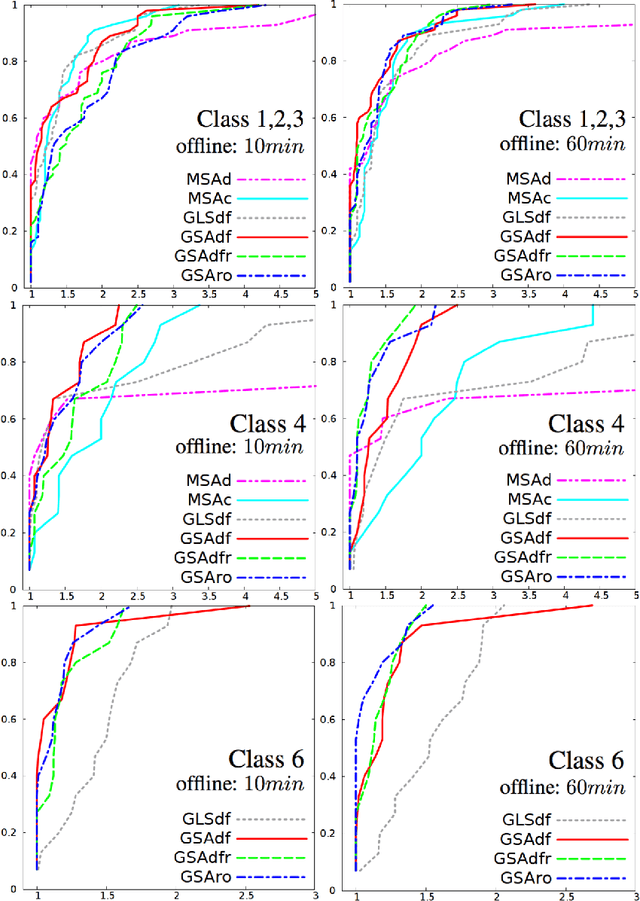
We consider a dynamic vehicle routing problem with time windows and stochastic customers (DS-VRPTW), such that customers may request for services as vehicles have already started their tours. To solve this problem, the goal is to provide a decision rule for choosing, at each time step, the next action to perform in light of known requests and probabilistic knowledge on requests likelihood. We introduce a new decision rule, called Global Stochastic Assessment (GSA) rule for the DS-VRPTW, and we compare it with existing decision rules, such as MSA. In particular, we show that GSA fully integrates nonanticipativity constraints so that it leads to better decisions in our stochastic context. We describe a new heuristic approach for efficiently approximating our GSA rule. We introduce a new waiting strategy. Experiments on dynamic and stochastic benchmarks, which include instances of different degrees of dynamism, show that not only our approach is competitive with state-of-the-art methods, but also enables to compute meaningful offline solutions to fully dynamic problems where absolutely no a priori customer request is provided.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge