Transient anisotropic kernel for probabilistic learning on manifolds

PLoM (Probabilistic Learning on Manifolds) is a method introduced in 2016 for handling small training datasets by projecting an It\^o equation from a stochastic dissipative Hamiltonian dynamical system, acting as the MCMC generator, for which the KDE-estimated probability measure with the training dataset is the invariant measure. PLoM performs a projection on a reduced-order vector basis related to the training dataset, using the diffusion maps (DMAPS) basis constructed with a time-independent isotropic kernel. In this paper, we propose a new ISDE projection vector basis built from a transient anisotropic kernel, providing an alternative to the DMAPS basis to improve statistical surrogates for stochastic manifolds with heterogeneous data. The construction ensures that for times near the initial time, the DMAPS basis coincides with the transient basis. For larger times, the differences between the two bases are characterized by the angle of their spanned vector subspaces. The optimal instant yielding the optimal transient basis is determined using an estimation of mutual information from Information Theory, which is normalized by the entropy estimation to account for the effects of the number of realizations used in the estimations. Consequently, this new vector basis better represents statistical dependencies in the learned probability measure for any dimension. Three applications with varying levels of statistical complexity and data heterogeneity validate the proposed theory, showing that the transient anisotropic kernel improves the learned probability measure.

Probabilistic learning constrained by realizations using a weak formulation of Fourier transform of probability measures

This paper deals with the taking into account a given set of realizations as constraints in the Kullback-Leibler minimum principle, which is used as a probabilistic learning algorithm. This permits the effective integration of data into predictive models. We consider the probabilistic learning of a random vector that is made up of either a quantity of interest (unsupervised case) or the couple of the quantity of interest and a control parameter (supervised case). A training set of independent realizations of this random vector is assumed to be given and to be generated with a prior probability measure that is unknown. A target set of realizations of the QoI is available for the two considered cases. The framework is the one of non-Gaussian problems in high dimension. A functional approach is developed on the basis of a weak formulation of the Fourier transform of probability measures (characteristic functions). The construction makes it possible to take into account the target set of realizations of the QoI in the Kullback-Leibler minimum principle. The proposed approach allows for estimating the posterior probability measure of the QoI (unsupervised case) or of the posterior joint probability measure of the QoI with the control parameter (supervised case). The existence and the uniqueness of the posterior probability measure is analyzed for the two cases. The numerical aspects are detailed in order to facilitate the implementation of the proposed method. The presented application in high dimension demonstrates the efficiency and the robustness of the proposed algorithm.

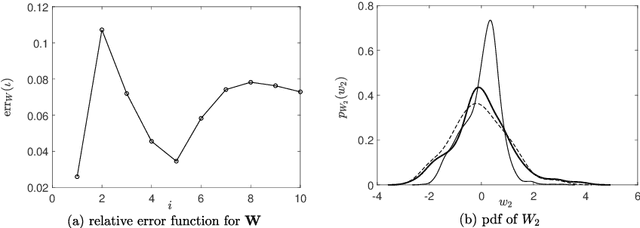
Probabilistic learning inference of boundary value problem with uncertainties based on Kullback-Leibler divergence under implicit constraints

In a first part, we present a mathematical analysis of a general methodology of a probabilistic learning inference that allows for estimating a posterior probability model for a stochastic boundary value problem from a prior probability model. The given targets are statistical moments for which the underlying realizations are not available. Under these conditions, the Kullback-Leibler divergence minimum principle is used for estimating the posterior probability measure. A statistical surrogate model of the implicit mapping, which represents the constraints, is introduced. The MCMC generator and the necessary numerical elements are given to facilitate the implementation of the methodology in a parallel computing framework. In a second part, an application is presented to illustrate the proposed theory and is also, as such, a contribution to the three-dimensional stochastic homogenization of heterogeneous linear elastic media in the case of a non-separation of the microscale and macroscale. For the construction of the posterior probability measure by using the probabilistic learning inference, in addition to the constraints defined by given statistical moments of the random effective elasticity tensor, the second-order moment of the random normalized residue of the stochastic partial differential equation has been added as a constraint. This constraint guarantees that the algorithm seeks to bring the statistical moments closer to their targets while preserving a small residue.

Probabilistic learning on manifolds constrained by nonlinear partial differential equations for small datasets

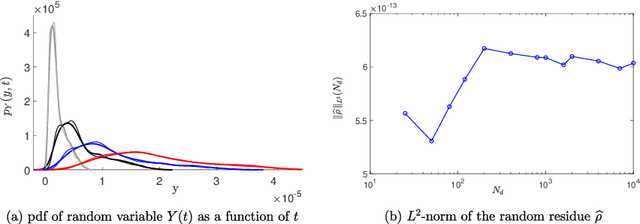
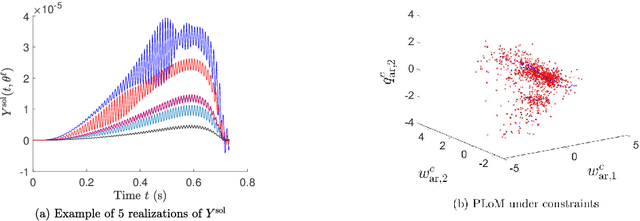
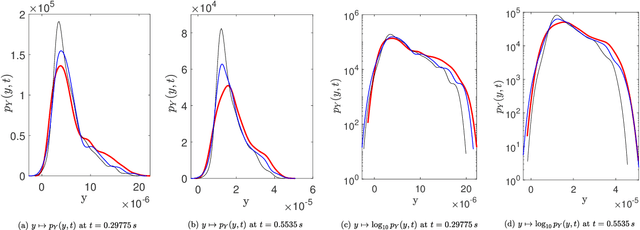
A novel extension of the Probabilistic Learning on Manifolds (PLoM) is presented. It makes it possible to synthesize solutions to a wide range of nonlinear stochastic boundary value problems described by partial differential equations (PDEs) for which a stochastic computational model (SCM) is available and depends on a vector-valued random control parameter. The cost of a single numerical evaluation of this SCM is assumed to be such that only a limited number of points can be computed for constructing the training dataset (small data). Each point of the training dataset is made up realizations from a vector-valued stochastic process (the stochastic solution) and the associated random control parameter on which it depends. The presented PLoM constrained by PDE allows for generating a large number of learned realizations of the stochastic process and its corresponding random control parameter. These learned realizations are generated so as to minimize the vector-valued random residual of the PDE in the mean-square sense. Appropriate novel methods are developed to solve this challenging problem. Three applications are presented. The first one is a simple uncertain nonlinear dynamical system with a nonstationary stochastic excitation. The second one concerns the 2D nonlinear unsteady Navier-Stokes equations for incompressible flows in which the Reynolds number is the random control parameter. The last one deals with the nonlinear dynamics of a 3D elastic structure with uncertainties. The results obtained make it possible to validate the PLoM constrained by stochastic PDE but also provide further validation of the PLoM without constraint.

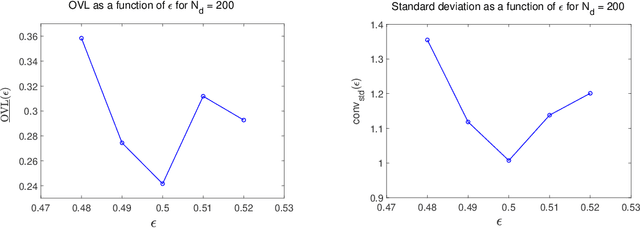
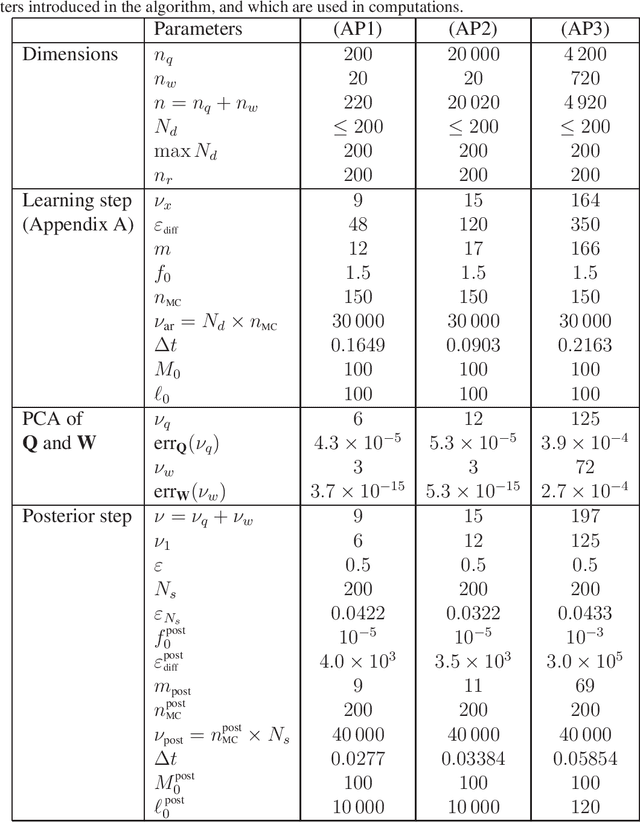
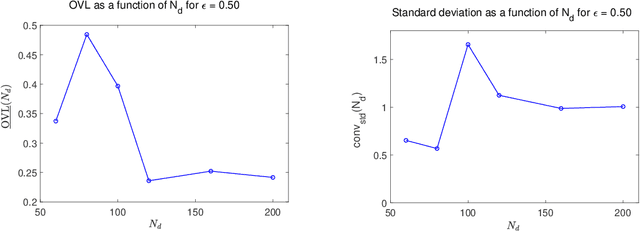
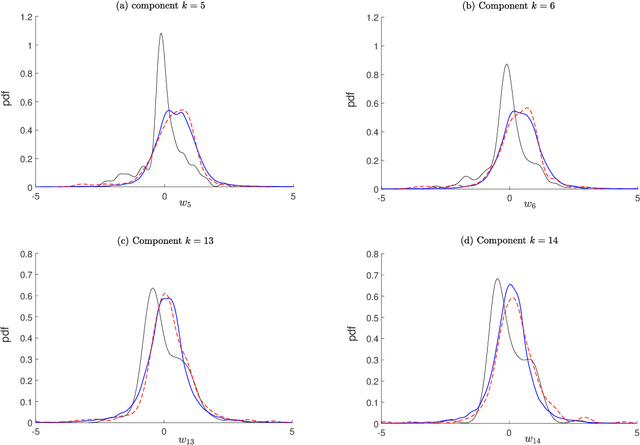
Sampling of Bayesian posteriors with a non-Gaussian probabilistic learning on manifolds from a small dataset

This paper tackles the challenge presented by small-data to the task of Bayesian inference. A novel methodology, based on manifold learning and manifold sampling, is proposed for solving this computational statistics problem under the following assumptions: 1) neither the prior model nor the likelihood function are Gaussian and neither can be approximated by a Gaussian measure; 2) the number of functional input (system parameters) and functional output (quantity of interest) can be large; 3) the number of available realizations of the prior model is small, leading to the small-data challenge typically associated with expensive numerical simulations; the number of experimental realizations is also small; 4) the number of the posterior realizations required for decision is much larger than the available initial dataset. The method and its mathematical aspects are detailed. Three applications are presented for validation: The first two involve mathematical constructions aimed to develop intuition around the method and to explore its performance. The third example aims to demonstrate the operational value of the method using a more complex application related to the statistical inverse identification of the non-Gaussian matrix-valued random elasticity field of a damaged biological tissue (osteoporosis in a cortical bone) using ultrasonic waves.