Probabilistic learning on manifolds constrained by nonlinear partial differential equations for small datasets

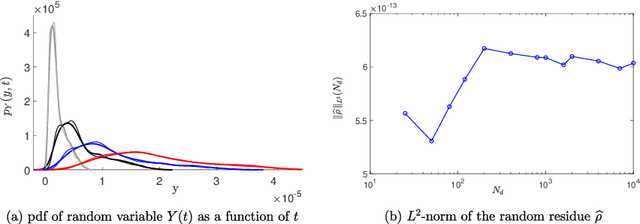
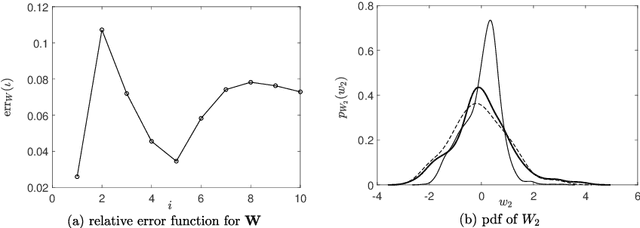
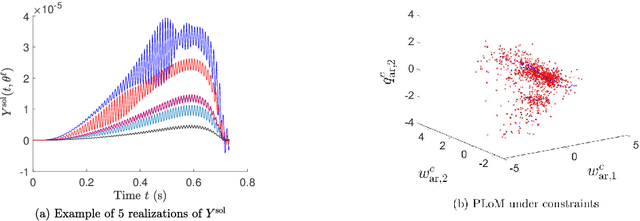
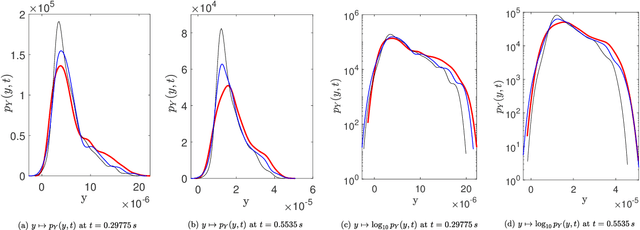
A novel extension of the Probabilistic Learning on Manifolds (PLoM) is presented. It makes it possible to synthesize solutions to a wide range of nonlinear stochastic boundary value problems described by partial differential equations (PDEs) for which a stochastic computational model (SCM) is available and depends on a vector-valued random control parameter. The cost of a single numerical evaluation of this SCM is assumed to be such that only a limited number of points can be computed for constructing the training dataset (small data). Each point of the training dataset is made up realizations from a vector-valued stochastic process (the stochastic solution) and the associated random control parameter on which it depends. The presented PLoM constrained by PDE allows for generating a large number of learned realizations of the stochastic process and its corresponding random control parameter. These learned realizations are generated so as to minimize the vector-valued random residual of the PDE in the mean-square sense. Appropriate novel methods are developed to solve this challenging problem. Three applications are presented. The first one is a simple uncertain nonlinear dynamical system with a nonstationary stochastic excitation. The second one concerns the 2D nonlinear unsteady Navier-Stokes equations for incompressible flows in which the Reynolds number is the random control parameter. The last one deals with the nonlinear dynamics of a 3D elastic structure with uncertainties. The results obtained make it possible to validate the PLoM constrained by stochastic PDE but also provide further validation of the PLoM without constraint.