Chenhua Geng
Differentiable Programming of Isometric Tensor Networks
Nov 01, 2021
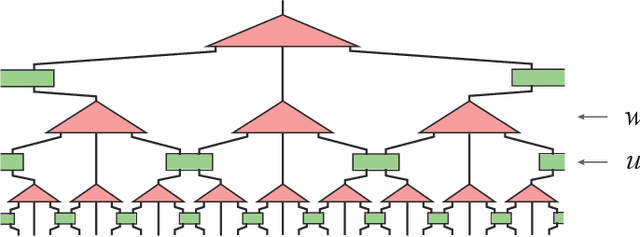
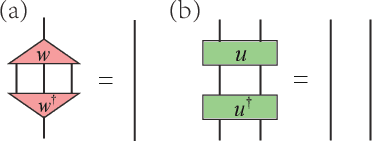
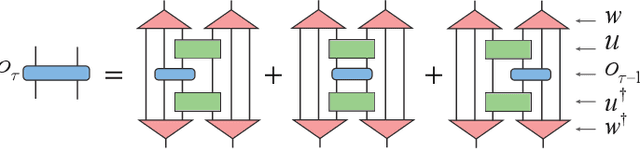
Abstract:Differentiable programming is a new programming paradigm which enables large scale optimization through automatic calculation of gradients also known as auto-differentiation. This concept emerges from deep learning, and has also been generalized to tensor network optimizations. Here, we extend the differentiable programming to tensor networks with isometric constraints with applications to multiscale entanglement renormalization ansatz (MERA) and tensor network renormalization (TNR). By introducing several gradient-based optimization methods for the isometric tensor network and comparing with Evenbly-Vidal method, we show that auto-differentiation has a better performance for both stability and accuracy. We numerically tested our methods on 1D critical quantum Ising spin chain and 2D classical Ising model. We calculate the ground state energy for the 1D quantum model and internal energy for the classical model, and scaling dimensions of scaling operators and find they all agree with the theory well.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge