Chengzuo Zhuge
Deep learning for predicting the occurrence of tipping points
Jul 26, 2024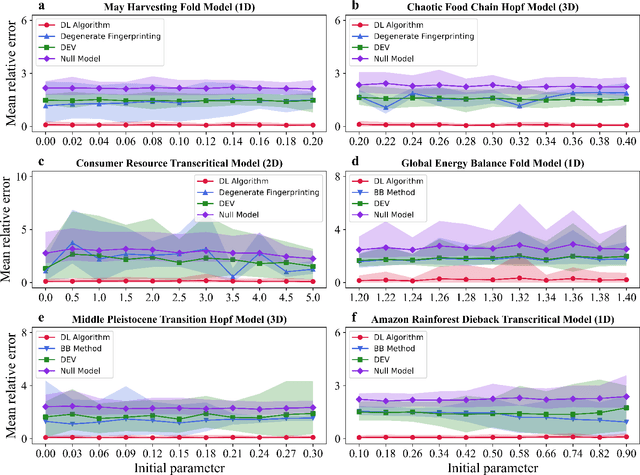
Abstract:Tipping points occur in many real-world systems, at which the system shifts suddenly from one state to another. The ability to predict the occurrence of tipping points from time series data remains an outstanding challenge and a major interest in a broad range of research fields. Particularly, the widely used methods based on bifurcation theory are neither reliable in prediction accuracy nor applicable for irregularly-sampled time series which are commonly observed from real-world systems. Here we address this challenge by developing a deep learning algorithm for predicting the occurrence of tipping points in untrained systems, by exploiting information about normal forms. Our algorithm not only outperforms traditional methods for regularly-sampled model time series but also achieves accurate predictions for irregularly-sampled model time series and empirical time series. Our ability to predict tipping points for complex systems paves the way for mitigation risks, prevention of catastrophic failures, and restoration of degraded systems, with broad applications in social science, engineering, and biology.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge