Chencheng Cai
KoPA: Automated Kronecker Product Approximation
Dec 17, 2019
Abstract:We consider the matrix approximation induced by the Kronecker product decomposition. We propose to approximate a given matrix by the sum of a few Kronecker products, which we refer to as the Kronecker product approximation (KoPA). Because the Kronecker product is an extensions of the outer product from vectors to matrices, KoPA extends the low rank approximation, and include the latter as a special case. KoPA also offers a greater flexibility over the low rank approximation, since it allows the user to choose the configuration, which are the dimensions of the two smaller matrices forming the Kronecker product. On the other hand, the configuration to be used is usually unknown, and has to be determined from the data in order to achieve the optimal balance between accuracy and parsimony. We propose to use extended information criteria to select the configuration. Under the paradigm of high dimensional analysis, we show that the proposed procedure is able to select the true configuration with probability tending to one, under suitable conditions on the signal-to-noise ratio. We demonstrate the superiority of KoPA over the low rank approximations through numerical studies, and a benchmark image example.
Stable Matrix Completion using Properly Configured Kronecker Product Decomposition
Dec 06, 2019



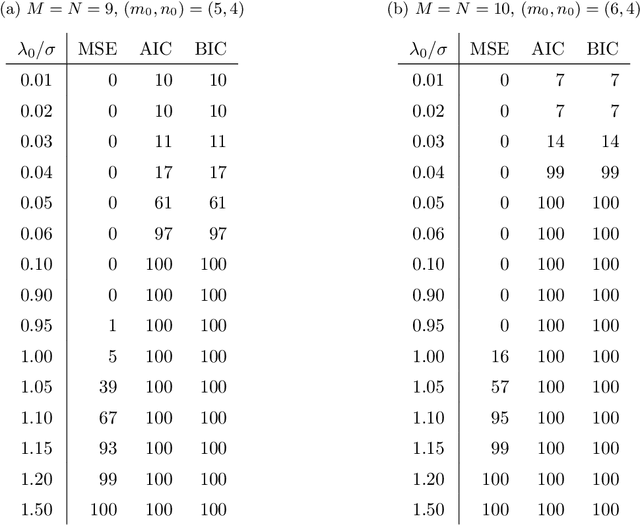
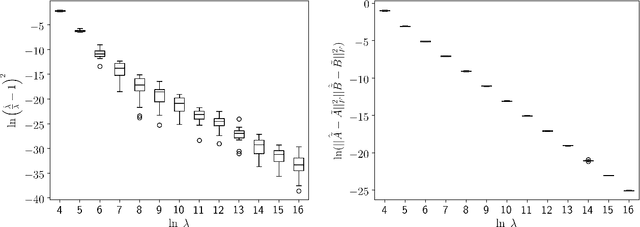
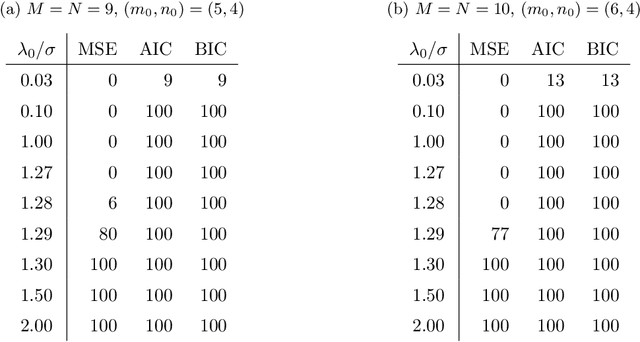
Abstract:Matrix completion problems are the problems of recovering missing entries in a partially observed high dimensional matrix with or without noise. Such a problem is encountered in a wide range of applications such as collaborative filtering, global positioning and remote sensing. Most of the existing matrix completion algorithms assume a low rank structure of the underlying complete matrix and perform reconstruction through the recovery of the low-rank structure using singular value decomposition. In this paper, we propose an alternative and more flexible structure for the underlying true complete matrix for the purpose of matrix completion and denoising. Specifically, instead of assuming a low matrix rank, we assume the underlying complete matrix has a low Kronecker product rank structure. Such a structure is often seen in the matrix observations in signal processing and image processing applications. The Kronecker product structure also includes low rank singular value decomposition structure commonly used as one of its special cases. The extra flexibility assumed for the underlying structure allows for using much less number of parameters but also raises the challenge of determining the proper Kronecker product configuration to be used. In this article, we propose to use a class of information criteria for the determination of the proper configuration and study its empirical performance in matrix completion problems. Simulation studies show promising results that the true underlying configuration can be accurately selected by the information criteria and the accompanying matrix completion algorithm can produce more accurate matrix recovery with less number of parameters than the standard matrix completion algorithms.
Hybrid Kronecker Product Decomposition and Approximation
Dec 06, 2019



Abstract:Discovering the underlying low dimensional structure of high dimensional data has attracted a significant amount of researches recently and has shown to have a wide range of applications. As an effective dimension reduction tool, singular value decomposition is often used to analyze high dimensional matrices, which are traditionally assumed to have a low rank matrix approximation. In this paper, we propose a new approach. We assume a high dimensional matrix can be approximated by a sum of a small number of Kronecker products of matrices with potentially different configurations, named as a hybird Kronecker outer Product Approximation (hKoPA). It provides an extremely flexible way of dimension reduction compared to the low-rank matrix approximation. Challenges arise in estimating a hKoPA when the configurations of component Kronecker products are different or unknown. We propose an estimation procedure when the set of configurations are given and a joint configuration determination and component estimation procedure when the configurations are unknown. Specifically, a least squares backfitting algorithm is used when the configuration is given. When the configuration is unknown, an iterative greedy algorithm is used. Both simulation and real image examples show that the proposed algorithms have promising performances. The hybrid Kronecker product approximation may have potentially wider applications in low dimensional representation of high dimensional data
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge