KoPA: Automated Kronecker Product Approximation

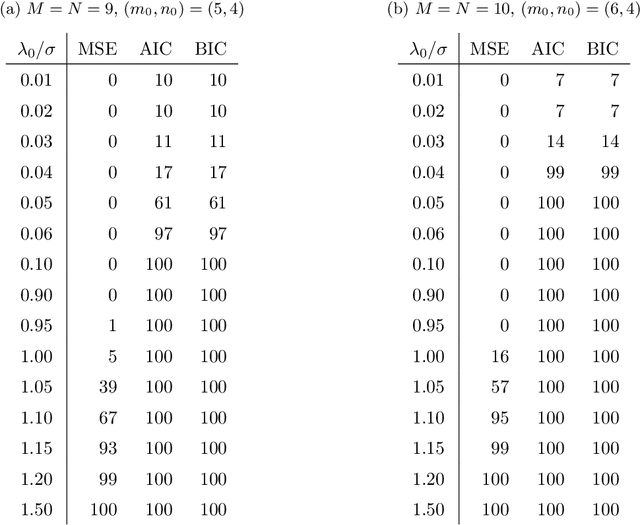
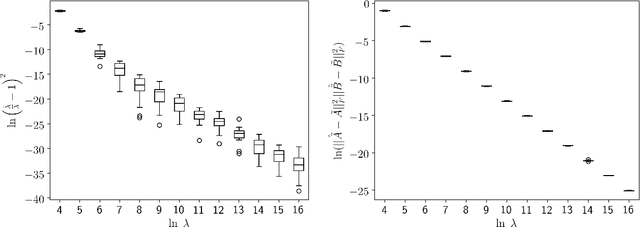
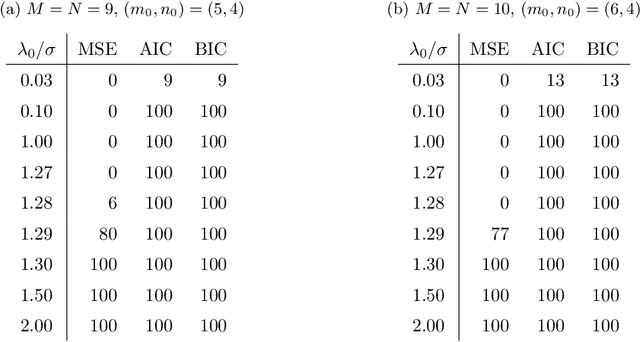
We consider the matrix approximation induced by the Kronecker product decomposition. We propose to approximate a given matrix by the sum of a few Kronecker products, which we refer to as the Kronecker product approximation (KoPA). Because the Kronecker product is an extensions of the outer product from vectors to matrices, KoPA extends the low rank approximation, and include the latter as a special case. KoPA also offers a greater flexibility over the low rank approximation, since it allows the user to choose the configuration, which are the dimensions of the two smaller matrices forming the Kronecker product. On the other hand, the configuration to be used is usually unknown, and has to be determined from the data in order to achieve the optimal balance between accuracy and parsimony. We propose to use extended information criteria to select the configuration. Under the paradigm of high dimensional analysis, we show that the proposed procedure is able to select the true configuration with probability tending to one, under suitable conditions on the signal-to-noise ratio. We demonstrate the superiority of KoPA over the low rank approximations through numerical studies, and a benchmark image example.