Fast Diffusion EM: a diffusion model for blind inverse problems with application to deconvolution

Using diffusion models to solve inverse problems is a growing field of research. Current methods assume the degradation to be known and provide impressive results in terms of restoration quality and diversity. In this work, we leverage the efficiency of those models to jointly estimate the restored image and unknown parameters of the degradation model. In particular, we designed an algorithm based on the well-known Expectation-Minimization (EM) estimation method and diffusion models. Our method alternates between approximating the expected log-likelihood of the inverse problem using samples drawn from a diffusion model and a maximization step to estimate unknown model parameters. For the maximization step, we also introduce a novel blur kernel regularization based on a Plug \& Play denoiser. Diffusion models are long to run, thus we provide a fast version of our algorithm. Extensive experiments on blind image deblurring demonstrate the effectiveness of our method when compared to other state-of-the-art approaches.

Provably Convergent Plug & Play Linearized ADMM, applied to Deblurring Spatially Varying Kernels

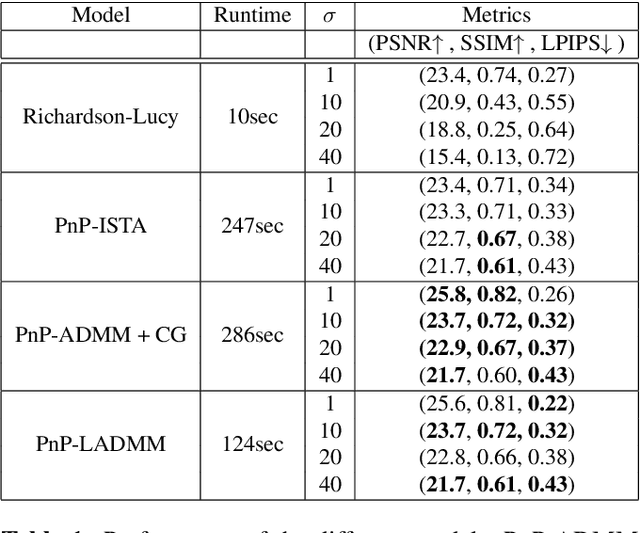
Plug & Play methods combine proximal algorithms with denoiser priors to solve inverse problems. These methods rely on the computability of the proximal operator of the data fidelity term. In this paper, we propose a Plug & Play framework based on linearized ADMM that allows us to bypass the computation of intractable proximal operators. We demonstrate the convergence of the algorithm and provide results on restoration tasks such as super-resolution and deblurring with non-uniform blur.

Deep Model-Based Super-Resolution with Non-uniform Blur

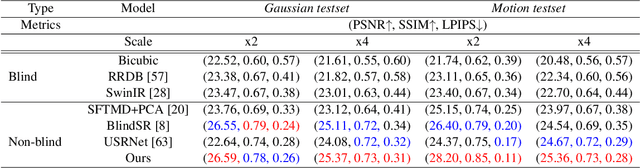
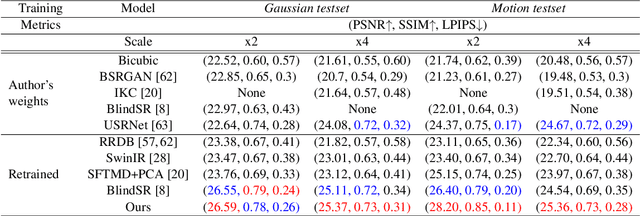
We propose a state-of-the-art method for super-resolution with non-uniform blur. Single-image super-resolution methods seek to restore a high-resolution image from blurred, subsampled, and noisy measurements. Despite their impressive performance, existing techniques usually assume a uniform blur kernel. Hence, these techniques do not generalize well to the more general case of non-uniform blur. Instead, in this paper, we address the more realistic and computationally challenging case of spatially-varying blur. To this end, we first propose a fast deep plug-and-play algorithm, based on linearized ADMM splitting techniques, which can solve the super-resolution problem with spatially-varying blur. Second, we unfold our iterative algorithm into a single network and train it end-to-end. In this way, we overcome the intricacy of manually tuning the parameters involved in the optimization scheme. Our algorithm presents remarkable performance and generalizes well after a single training to a large family of spatially-varying blur kernels, noise levels and scale factors.