Chang-Shen Lee
Finite-Bit Quantization For Distributed Algorithms With Linear Convergence
Jul 23, 2021
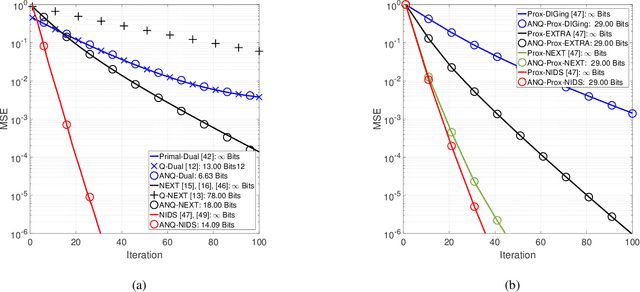
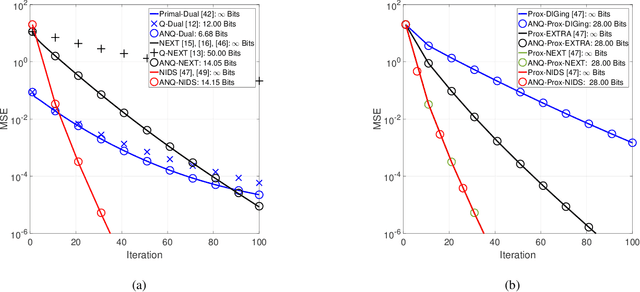

Abstract:This paper studies distributed algorithms for (strongly convex) composite optimization problems over mesh networks, subject to quantized communications. Instead of focusing on a specific algorithmic design, we propose a black-box model casting distributed algorithms in the form of fixed-point iterates, converging at linear rate. The algorithmic model is coupled with a novel (random) Biased Compression (BC-)rule on the quantizer design, which preserves linear convergence. A new quantizer coupled with a communication-efficient encoding scheme is also proposed, which efficiently implements the BC-rule using a finite number of bits. This contrasts with most of existing quantization rules, whose implementation calls for an infinite number of bits. A unified communication complexity analysis is developed for the black-box model, determining the average number of bit required to reach a solution of the optimization problem within the required accuracy. Numerical results validate our theoretical findings and show that distributed algorithms equipped with the proposed quantizer have more favorable communication complexity than algorithms using existing quantization rules.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge