Fully Adaptive Regret-Guaranteed Algorithm for Control of Linear Quadratic Systems

The first algorithm for the Linear Quadratic (LQ) control problem with an unknown system model, featuring a regret of $\mathcal{O}(\sqrt{T})$, was introduced by Abbasi-Yadkori and Szepesv\'ari (2011). Recognizing the computational complexity of this algorithm, subsequent efforts (see Cohen et al. (2019), Mania et al. (2019), Faradonbeh et al. (2020a), and Kargin et al.(2022)) have been dedicated to proposing algorithms that are computationally tractable while preserving this order of regret. Although successful, the existing works in the literature lack a fully adaptive exploration-exploitation trade-off adjustment and require a user-defined value, which can lead to overall regret bound growth with some factors. In this work, noticing this gap, we propose the first fully adaptive algorithm that controls the number of policy updates (i.e., tunes the exploration-exploitation trade-off) and optimizes the upper-bound of regret adaptively. Our proposed algorithm builds on the SDP-based approach of Cohen et al. (2019) and relaxes its need for a horizon-dependant warm-up phase by appropriately tuning the regularization parameter and adding an adaptive input perturbation. We further show that through careful exploration-exploitation trade-off adjustment there is no need to commit to the widely-used notion of strong sequential stability, which is restrictive and can introduce complexities in initialization.

Online Decision Making with History-Average Dependent Costs (Extended)

In many online sequential decision-making scenarios, a learner's choices affect not just their current costs but also the future ones. In this work, we look at one particular case of such a situation where the costs depend on the time average of past decisions over a history horizon. We first recast this problem with history dependent costs as a problem of decision making under stage-wise constraints. To tackle this, we then propose the novel Follow-The-Adaptively-Regularized-Leader (FTARL) algorithm. Our innovative algorithm incorporates adaptive regularizers that depend explicitly on past decisions, allowing us to enforce stage-wise constraints while simultaneously enabling us to establish tight regret bounds. We also discuss the implications of the length of history horizon on design of no-regret algorithms for our problem and present impossibility results when it is the full learning horizon.

Pointwise-in-Time Explanation for Linear Temporal Logic Rules

This work introduces a framework to assess the relevance of individual linear temporal logic (LTL) constraints at specific times in a given path plan, a task we refer to as "pointwise-in-time" explanation. We develop this framework, featuring a status assessment algorithm, for agents which execute finite plans in a discrete-time, discrete-space setting expressible via a Kripke structure. Given a plan on this structure and a set of LTL rules which are known to constrain the agent, the algorithm responds to two types of user queries to produce explanation. For the selected query time, explanations identify which rules are active, which have just been satisfied, and which are inactive, where the framework status criteria are formally and intuitively defined. Explanations may also include the status of individual rule arguments to provide further insight. In this paper, we systematically present this novel framework and provide an example of its implementation.

On Estimating Multi-Attribute Choice Preferences using Private Signals and Matrix Factorization

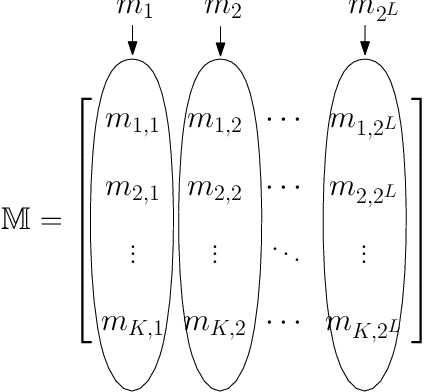
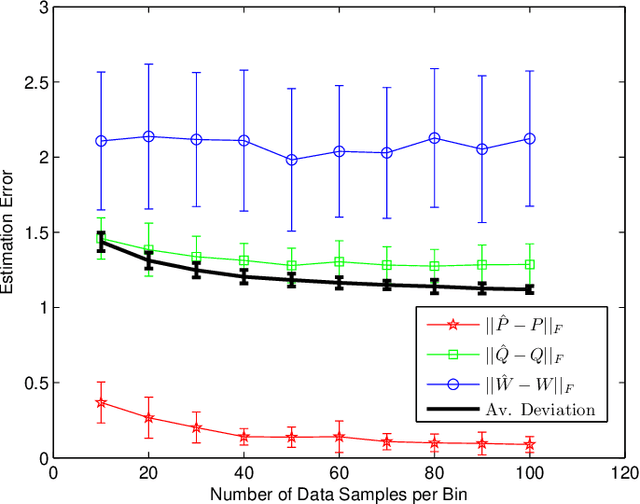
Revealed preference theory studies the possibility of modeling an agent's revealed preferences and the construction of a consistent utility function. However, modeling agent's choices over preference orderings is not always practical and demands strong assumptions on human rationality and data-acquisition abilities. Therefore, we propose a simple generative choice model where agents are assumed to generate the choice probabilities based on latent factor matrices that capture their choice evaluation across multiple attributes. Since the multi-attribute evaluation is typically hidden within the agent's psyche, we consider a signaling mechanism where agents are provided with choice information through private signals, so that the agent's choices provide more insight about his/her latent evaluation across multiple attributes. We estimate the choice model via a novel multi-stage matrix factorization algorithm that minimizes the average deviation of the factor estimates from choice data. Simulation results are presented to validate the estimation performance of our proposed algorithm.