Estimating nonlinear regression errors without doing regression

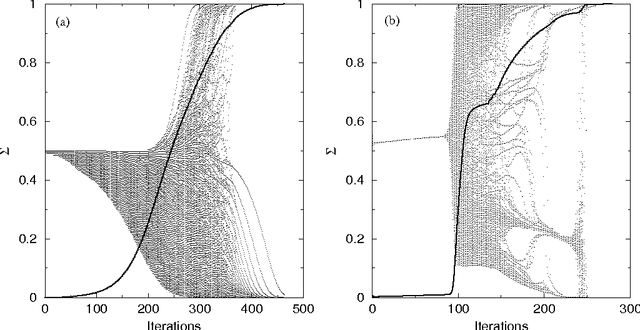
A method for estimating nonlinear regression errors and their distributions without performing regression is presented. Assuming continuity of the modeling function the variance is given in terms of conditional probabilities extracted from the data. For N data points the computational demand is N2. Comparing the predicted residual errors with those derived from a linear model assumption provides a signal for nonlinearity. The method is successfully illustrated with data generated by the Ikeda and Lorenz maps augmented with noise. As a by-product the embedding dimensions of these maps are also extracted.

An Efficient Mean Field Approach to the Set Covering Problem

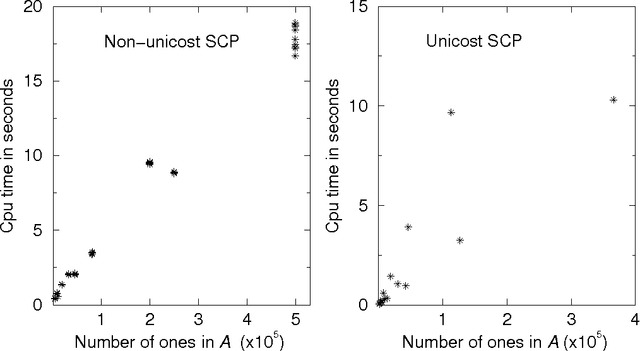
A mean field feedback artificial neural network algorithm is developed and explored for the set covering problem. A convenient encoding of the inequality constraints is achieved by means of a multilinear penalty function. An approximate energy minimum is obtained by iterating a set of mean field equations, in combination with annealing. The approach is numerically tested against a set of publicly available test problems with sizes ranging up to 5x10^3 rows and 10^6 columns. When comparing the performance with exact results for sizes where these are available, the approach yields results within a few percent from the optimal solutions. Comparisons with other approximate methods also come out well, in particular given the very low CPU consumption required -- typically a few seconds. Arbitrary problems can be processed using the algorithm via a public domain server.