Estimating causal effects of time-dependent exposures on a binary endpoint in a high-dimensional setting

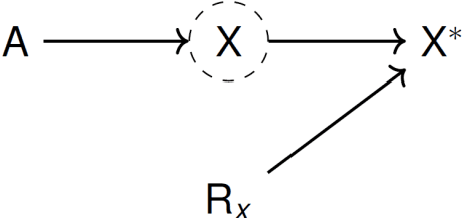
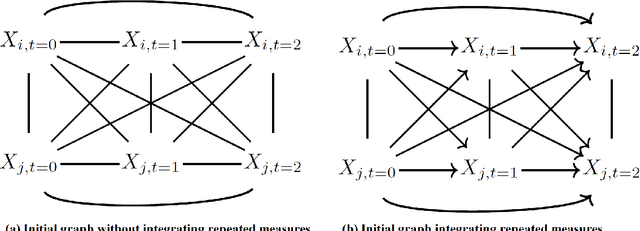
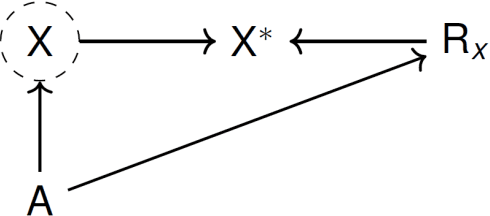
Recently, the intervention calculus when the DAG is absent (IDA) method was developed to estimate lower bounds of causal effects from observational high-dimensional data. Originally it was introduced to assess the effect of baseline biomarkers which do not vary over time. However, in many clinical settings, measurements of biomarkers are repeated at fixed time points during treatment exposure and, therefore, this method need to be extended. The purpose of this paper is then to extend the first step of the IDA, the Peter Clarks (PC)-algorithm, to a time-dependent exposure in the context of a binary outcome. We generalised the PC-algorithm for taking into account the chronological order of repeated measurements of the exposure and propose to apply the IDA with our new version, the chronologically ordered PC-algorithm (COPC-algorithm). A simulation study has been performed before applying the method for estimating causal effects of time-dependent immunological biomarkers on toxicity, death and progression in patients with metastatic melanoma. The simulation study showed that the completed partially directed acyclic graphs (CPDAGs) obtained using COPC-algorithm were structurally closer to the true CPDAG than CPDAGs obtained using PC-algorithm. Also, causal effects were more accurate when they were estimated based on CPDAGs obtained using COPC-algorithm. Moreover, CPDAGs obtained by COPC-algorithm allowed removing non-chronologic arrows with a variable measured at a time t pointing to a variable measured at a time t' where t'< t. Bidirected edges were less present in CPDAGs obtained with the COPC-algorithm, supporting the fact that there was less variability in causal effects estimated from these CPDAGs. The COPC-algorithm provided CPDAGs that keep the chronological structure present in the data, thus allowed to estimate lower bounds of the causal effect of time-dependent biomarkers.