Computational-Statistical Tradeoffs from NP-hardness

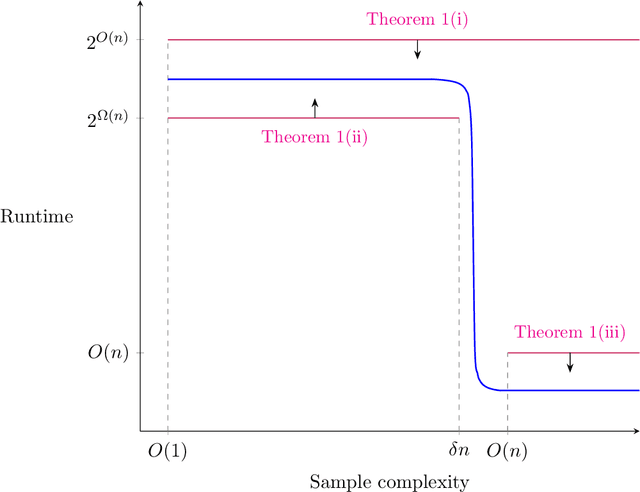
A central question in computer science and statistics is whether efficient algorithms can achieve the information-theoretic limits of statistical problems. Many computational-statistical tradeoffs have been shown under average-case assumptions, but since statistical problems are average-case in nature, it has been a challenge to base them on standard worst-case assumptions. In PAC learning where such tradeoffs were first studied, the question is whether computational efficiency can come at the cost of using more samples than information-theoretically necessary. We base such tradeoffs on $\mathsf{NP}$-hardness and obtain: $\circ$ Sharp computational-statistical tradeoffs assuming $\mathsf{NP}$ requires exponential time: For every polynomial $p(n)$, there is an $n$-variate class $C$ with VC dimension $1$ such that the sample complexity of time-efficiently learning $C$ is $\Theta(p(n))$. $\circ$ A characterization of $\mathsf{RP}$ vs. $\mathsf{NP}$ in terms of learning: $\mathsf{RP} = \mathsf{NP}$ iff every $\mathsf{NP}$-enumerable class is learnable with $O(\mathrm{VCdim}(C))$ samples in polynomial time. The forward implication has been known since (Pitt and Valiant, 1988); we prove the reverse implication. Notably, all our lower bounds hold against improper learners. These are the first $\mathsf{NP}$-hardness results for improperly learning a subclass of polynomial-size circuits, circumventing formal barriers of Applebaum, Barak, and Xiao (2008).

Superconstant Inapproximability of Decision Tree Learning

We consider the task of properly PAC learning decision trees with queries. Recent work of Koch, Strassle, and Tan showed that the strictest version of this task, where the hypothesis tree $T$ is required to be optimally small, is NP-hard. Their work leaves open the question of whether the task remains intractable if $T$ is only required to be close to optimal, say within a factor of 2, rather than exactly optimal. We answer this affirmatively and show that the task indeed remains NP-hard even if $T$ is allowed to be within any constant factor of optimal. More generally, our result allows for a smooth tradeoff between the hardness assumption and the inapproximability factor. As Koch et al.'s techniques do not appear to be amenable to such a strengthening, we first recover their result with a new and simpler proof, which we couple with a new XOR lemma for decision trees. While there is a large body of work on XOR lemmas for decision trees, our setting necessitates parameters that are extremely sharp, and are not known to be attainable by existing XOR lemmas. Our work also carries new implications for the related problem of Decision Tree Minimization.

Properly Learning Decision Trees with Queries Is NP-Hard

We prove that it is NP-hard to properly PAC learn decision trees with queries, resolving a longstanding open problem in learning theory (Bshouty 1993; Guijarro-Lavin-Raghavan 1999; Mehta-Raghavan 2002; Feldman 2016). While there has been a long line of work, dating back to (Pitt-Valiant 1988), establishing the hardness of properly learning decision trees from random examples, the more challenging setting of query learners necessitates different techniques and there were no previous lower bounds. En route to our main result, we simplify and strengthen the best known lower bounds for a different problem of Decision Tree Minimization (Zantema-Bodlaender 2000; Sieling 2003). On a technical level, we introduce the notion of hardness distillation, which we study for decision tree complexity but can be considered for any complexity measure: for a function that requires large decision trees, we give a general method for identifying a small set of inputs that is responsible for its complexity. Our technique even rules out query learners that are allowed constant error. This contrasts with existing lower bounds for the setting of random examples which only hold for inverse-polynomial error. Our result, taken together with a recent almost-polynomial time query algorithm for properly learning decision trees under the uniform distribution (Blanc-Lange-Qiao-Tan 2022), demonstrates the dramatic impact of distributional assumptions on the problem.

Superpolynomial Lower Bounds for Decision Tree Learning and Testing

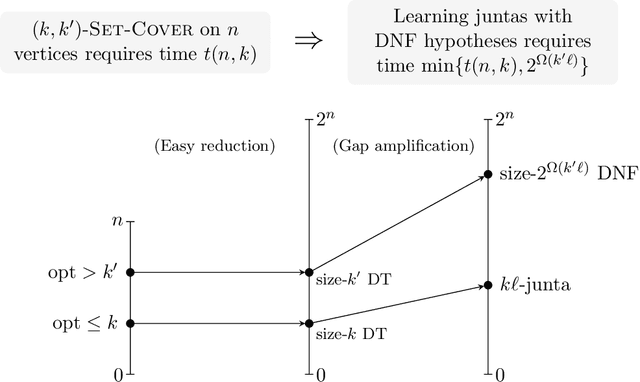
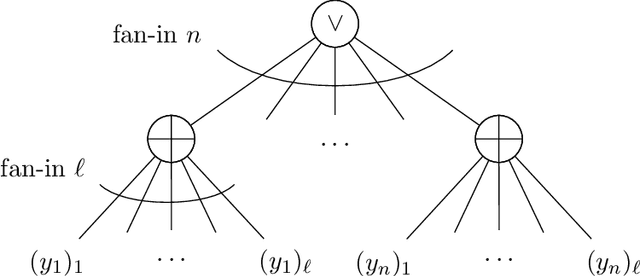
We establish new hardness results for decision tree optimization problems, adding to a line of work that dates back to Hyafil and Rivest in 1976. We prove, under randomized ETH, superpolynomial lower bounds for two basic problems: given an explicit representation of a function $f$ and a generator for a distribution $\mathcal{D}$, construct a small decision tree approximator for $f$ under $\mathcal{D}$, and decide if there is a small decision tree approximator for $f$ under $\mathcal{D}$. Our results imply new lower bounds for distribution-free PAC learning and testing of decision trees, settings in which the algorithm only has restricted access to $f$ and $\mathcal{D}$. Specifically, we show: $n$-variable size-$s$ decision trees cannot be properly PAC learned in time $n^{\tilde{O}(\log\log s)}$, and depth-$d$ decision trees cannot be tested in time $\exp(d^{\,O(1)})$. For learning, the previous best lower bound only ruled out $\text{poly}(n)$-time algorithms (Alekhnovich, Braverman, Feldman, Klivans, and Pitassi, 2009). For testing, recent work gives similar though incomparable bounds in the setting where $f$ is random and $\mathcal{D}$ is nonexplicit (Blais, Ferreira Pinto Jr., and Harms, 2021). Assuming a plausible conjecture on the hardness of Set-Cover, we show our lower bound for learning decision trees can be improved to $n^{\Omega(\log s)}$, matching the best known upper bound of $n^{O(\log s)}$ due to Ehrenfeucht and Haussler (1989). We obtain our results within a unified framework that leverages recent progress in two lines of work: the inapproximability of Set-Cover and XOR lemmas for query complexity. Our framework is versatile and yields results for related concept classes such as juntas and DNF formulas.