Superpolynomial Lower Bounds for Decision Tree Learning and Testing
Paper and Code
Oct 12, 2022
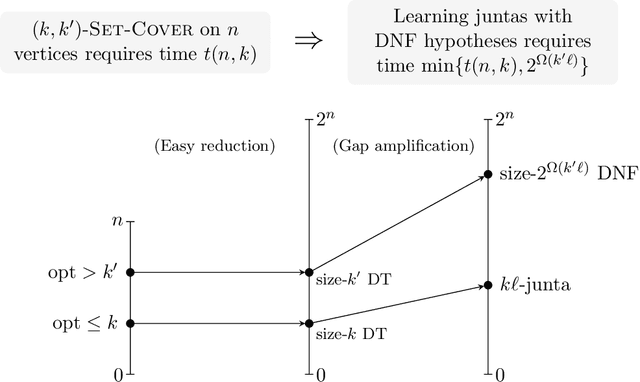

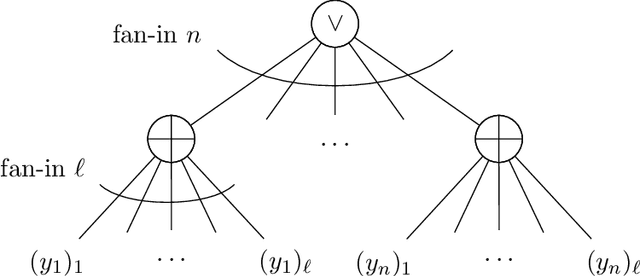
We establish new hardness results for decision tree optimization problems, adding to a line of work that dates back to Hyafil and Rivest in 1976. We prove, under randomized ETH, superpolynomial lower bounds for two basic problems: given an explicit representation of a function $f$ and a generator for a distribution $\mathcal{D}$, construct a small decision tree approximator for $f$ under $\mathcal{D}$, and decide if there is a small decision tree approximator for $f$ under $\mathcal{D}$. Our results imply new lower bounds for distribution-free PAC learning and testing of decision trees, settings in which the algorithm only has restricted access to $f$ and $\mathcal{D}$. Specifically, we show: $n$-variable size-$s$ decision trees cannot be properly PAC learned in time $n^{\tilde{O}(\log\log s)}$, and depth-$d$ decision trees cannot be tested in time $\exp(d^{\,O(1)})$. For learning, the previous best lower bound only ruled out $\text{poly}(n)$-time algorithms (Alekhnovich, Braverman, Feldman, Klivans, and Pitassi, 2009). For testing, recent work gives similar though incomparable bounds in the setting where $f$ is random and $\mathcal{D}$ is nonexplicit (Blais, Ferreira Pinto Jr., and Harms, 2021). Assuming a plausible conjecture on the hardness of Set-Cover, we show our lower bound for learning decision trees can be improved to $n^{\Omega(\log s)}$, matching the best known upper bound of $n^{O(\log s)}$ due to Ehrenfeucht and Haussler (1989). We obtain our results within a unified framework that leverages recent progress in two lines of work: the inapproximability of Set-Cover and XOR lemmas for query complexity. Our framework is versatile and yields results for related concept classes such as juntas and DNF formulas.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge