A Visual Entity-Relationship Model for Constraint-Based University Timetabling

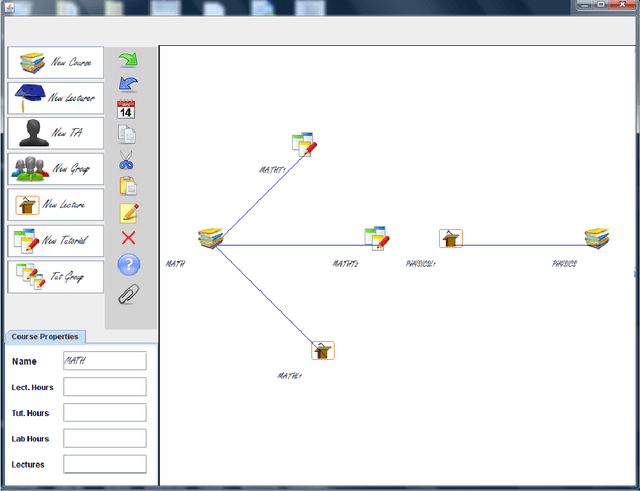
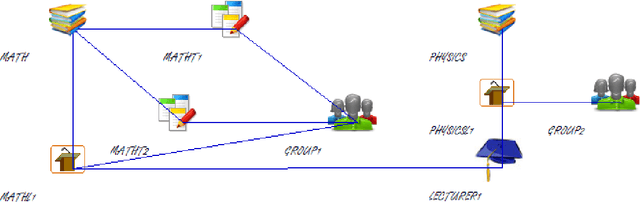
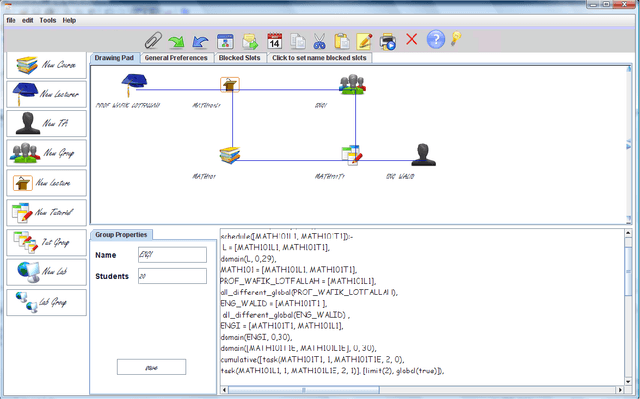
University timetabling (UTT) is a complex problem due to its combinatorial nature but also the type of constraints involved. The holy grail of (constraint) programming: "the user states the problem the program solves it" remains a challenge since solution quality is tightly coupled with deriving "effective models", best handled by technology experts. In this paper, focusing on the field of university timetabling, we introduce a visual graphic communication tool that lets the user specify her problem in an abstract manner, using a visual entity-relationship model. The entities are nodes of mainly two types: resource nodes (lecturers, assistants, student groups) and events nodes (lectures, lab sessions, tutorials). The links between the nodes signify a desired relationship between them. The visual modeling abstraction focuses on the nature of the entities and their relationships and abstracts from an actual constraint model.

Certainty Closure: Reliable Constraint Reasoning with Incomplete or Erroneous Data

Constraint Programming (CP) has proved an effective paradigm to model and solve difficult combinatorial satisfaction and optimisation problems from disparate domains. Many such problems arising from the commercial world are permeated by data uncertainty. Existing CP approaches that accommodate uncertainty are less suited to uncertainty arising due to incomplete and erroneous data, because they do not build reliable models and solutions guaranteed to address the user's genuine problem as she perceives it. Other fields such as reliable computation offer combinations of models and associated methods to handle these types of uncertain data, but lack an expressive framework characterising the resolution methodology independently of the model. We present a unifying framework that extends the CP formalism in both model and solutions, to tackle ill-defined combinatorial problems with incomplete or erroneous data. The certainty closure framework brings together modelling and solving methodologies from different fields into the CP paradigm to provide reliable and efficient approches for uncertain constraint problems. We demonstrate the applicability of the framework on a case study in network diagnosis. We define resolution forms that give generic templates, and their associated operational semantics, to derive practical solution methods for reliable solutions.