Carlos L. Benavides-Riveros
Neural Quantum Propagators for Driven-Dissipative Quantum Dynamics
Oct 21, 2024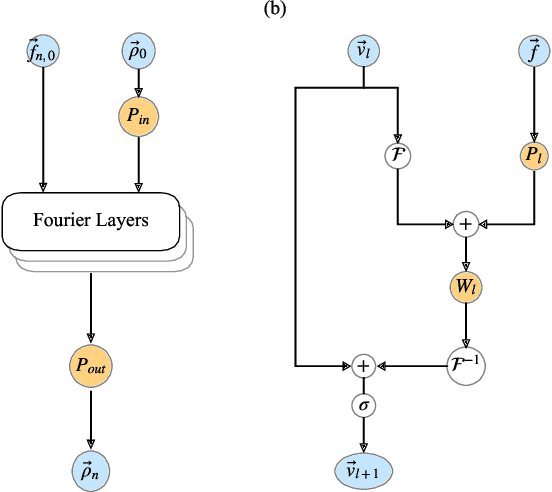
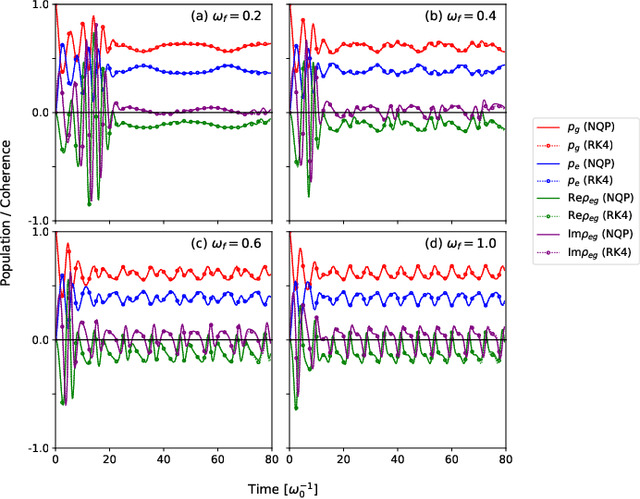
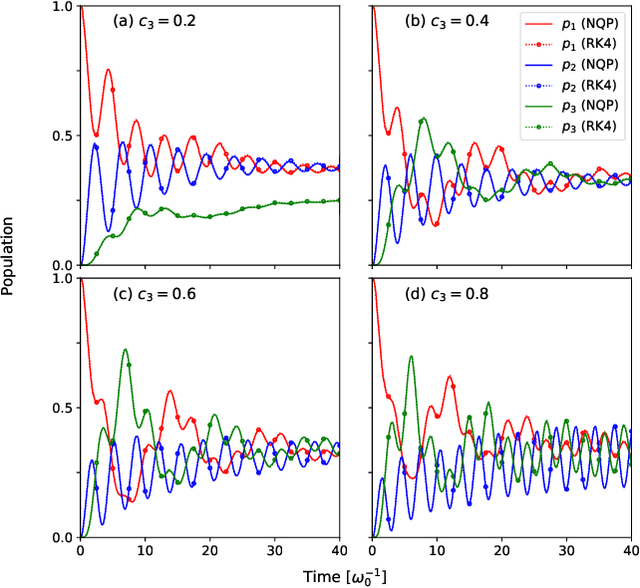
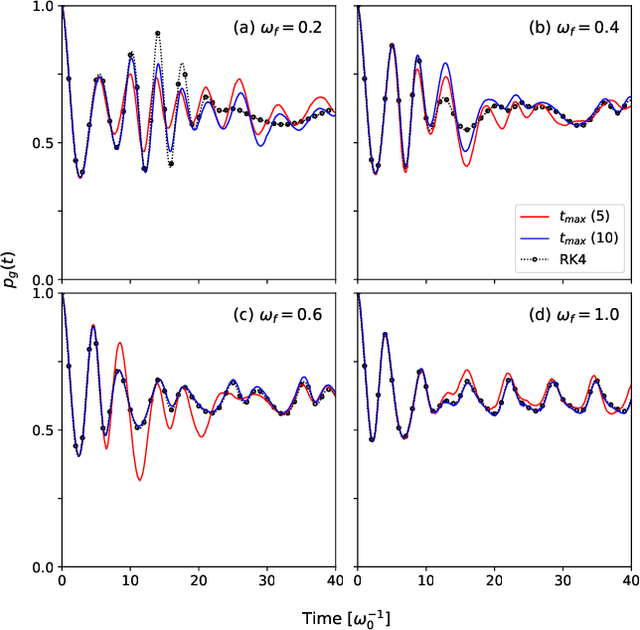
Abstract:Describing the dynamics of strong-laser driven open quantum systems is a very challenging task that requires the solution of highly involved equations of motion. While machine learning techniques are being applied with some success to simulate the time evolution of individual quantum states, their use to approximate time-dependent operators (that can evolve various states) remains largely unexplored. In this work, we develop driven neural quantum propagators (NQP), a universal neural network framework that solves driven-dissipative quantum dynamics by approximating propagators rather than wavefunctions or density matrices. NQP can handle arbitrary initial quantum states, adapt to various external fields, and simulate long-time dynamics, even when trained on far shorter time windows. Furthermore, by appropriately configuring the external fields, our trained NQP can be transferred to systems governed by different Hamiltonians. We demonstrate the effectiveness of our approach by studying the spin-boson and the three-state transition Gamma models.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge