The ML-EM algorithm in continuum: sparse measure solutions

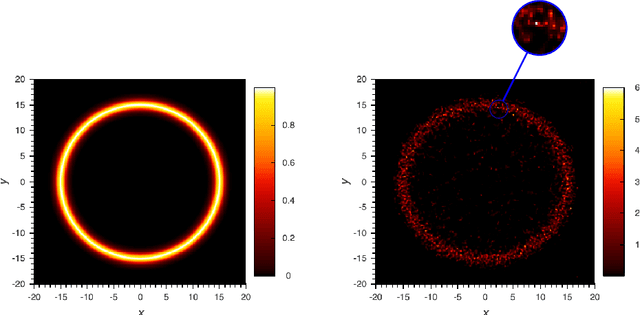
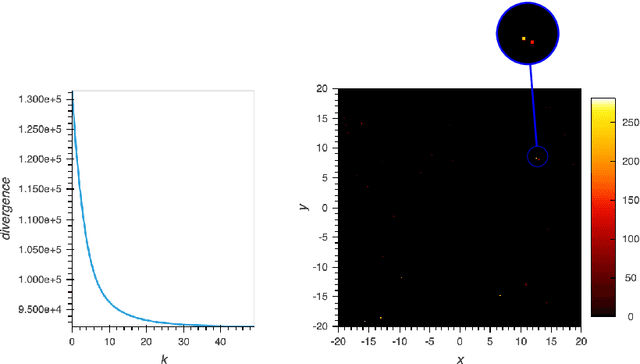
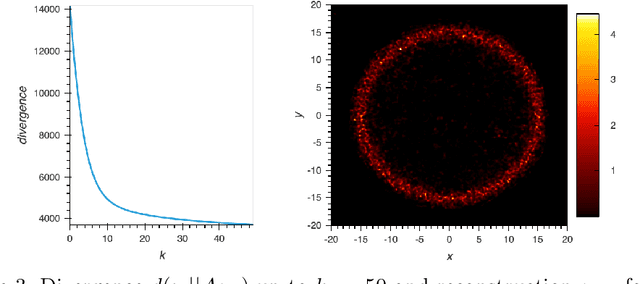
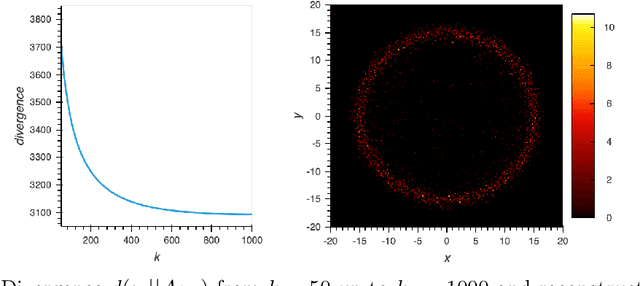
Linear inverse problems $A \mu = \delta$ with Poisson noise and non-negative unknown $\mu \geq 0$ are ubiquitous in applications, for instance in Positron Emission Tomography (PET) in medical imaging. The associated maximum likelihood problem is routinely solved using an expectation-maximisation algorithm (ML-EM). This typically results in images which look spiky, even with early stopping. We give an explanation for this phenomenon. We first regard the image $\mu$ as a measure. We prove that if the measurements $\delta$ are not in the cone $\{A \mu, \mu \geq 0\}$, which is typical of short exposure times, likelihood maximisers as well as ML-EM cluster points must be sparse, i.e., typically a sum of point masses. On the other hand, in the long exposure regime, we prove that cluster points of ML-EM will be measures without singular part. Finally, we provide concentration bounds for the probability to be in the sparse case.

Spatiotemporal PET reconstruction using ML-EM with learned diffeomorphic deformation

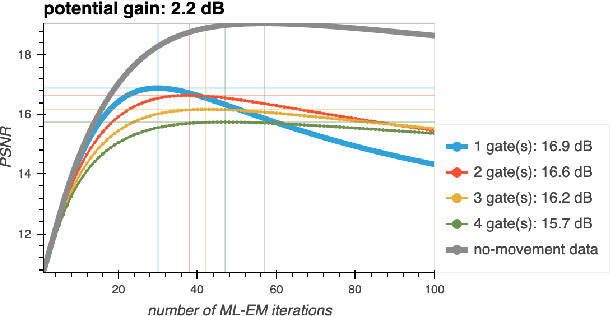
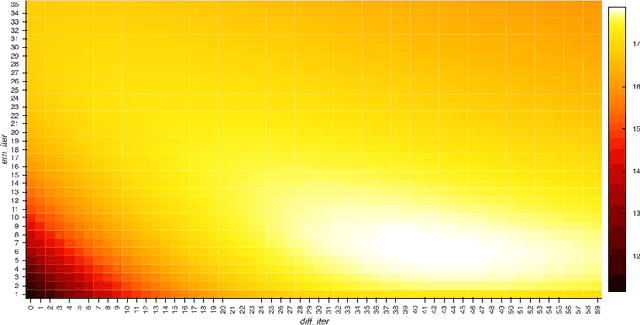
Patient movement in emission tomography deteriorates reconstruction quality because of motion blur. Gating the data improves the situation somewhat: each gate contains a movement phase which is approximately stationary. A standard method is to use only the data from a few gates, with little movement between them. However, the corresponding loss of data entails an increase of noise. Motion correction algorithms have been implemented to take into account all the gated data, but they do not scale well, especially not in 3D. We propose a novel motion correction algorithm which addresses the scalability issue. Our approach is to combine an enhanced ML-EM algorithm with deep learning based movement registration. The training is unsupervised, and with artificial data. We expect this approach to scale very well to higher resolutions and to 3D, as the overall cost of our algorithm is only marginally greater than that of a standard ML-EM algorithm. We show that we can significantly decrease the noise corresponding to a limited number of gates.