An efficient Lagrangian-based heuristic to solve a multi-objective sustainable supply chain problem

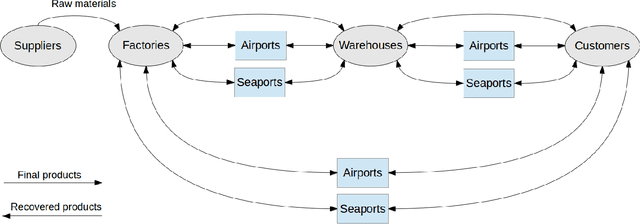
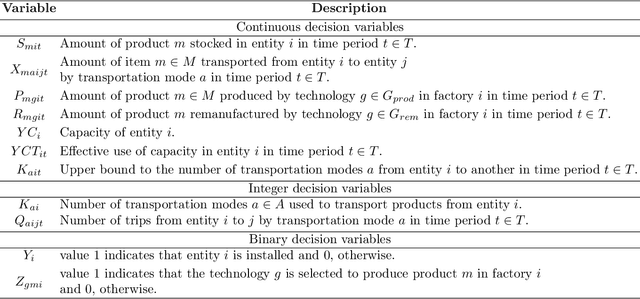
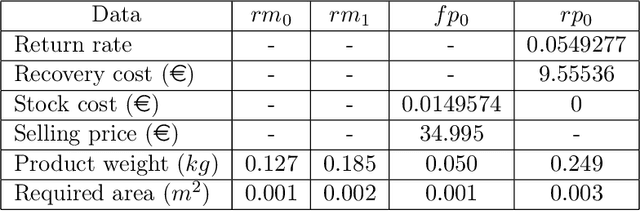
Sustainable Supply Chain (SSC) management aims at integrating economic, environmental and social goals to assist in the long-term planning of a company and its supply chains. There is no consensus in the literature as to whether social and environmental responsibilities are profit-compatible. However, the conflicting nature of these goals is explicit when considering specific assessment measures and, in this scenario, multi-objective optimization is a way to represent problems that simultaneously optimize the goals. This paper proposes a Lagrangian matheuristic method, called $AugMathLagr$, to solve a hard and relevant multi-objective problem found in the literature. $AugMathLagr$ was extensively tested using artificial instances defined by a generator presented in this paper. The results show a competitive performance of $AugMathLagr$ when compared with an exact multi-objective method limited by time and a matheuristic recently proposed in the literature and adapted here to address the studied problem. In addition, computational results on a case study are presented and analyzed, and demonstrate the outstanding performance of $AugMathLagr$.

An ensemble based on a bi-objective evolutionary spectral algorithm for graph clustering

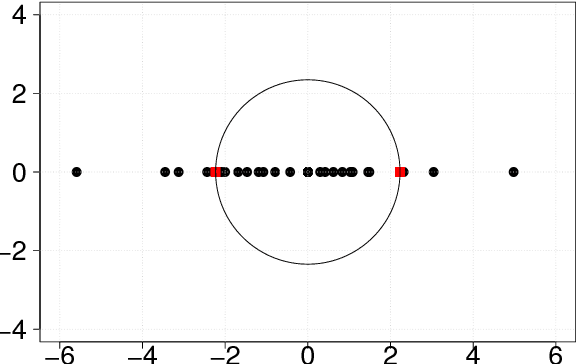
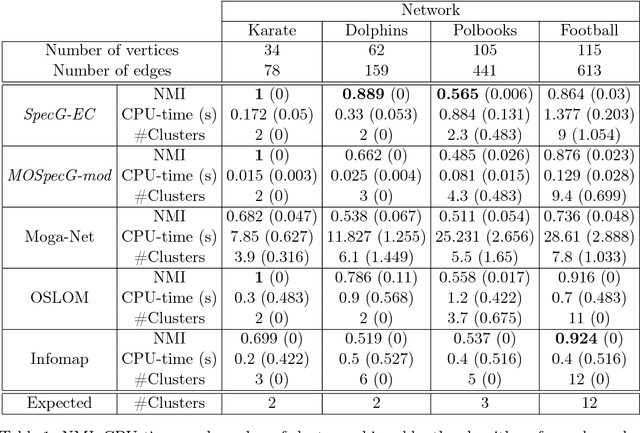
Graph clustering is a challenging pattern recognition problem whose goal is to identify vertex partitions with high intra-group connectivity. Because of the rough definition of this problem, there are numerous effective ways to formally determine such partitions. In particular, multi-objective optimization can deal with the trade-offs between different clustering quality measures in order to better assess the partitions. This paper investigates a problem that maximizes the number of intra-cluster edges of a graph and minimizes the expected number of inter-cluster edges in a random graph with the same degree sequence as the original one. The difference between the two investigated objectives is the definition of the well-known measure of graph clustering quality: the modularity. We introduce a spectral decomposition hybridized with an evolutionary heuristic, called MOSpecG, to approach this bi-objective problem and an ensemble strategy to consolidate the solutions found by MOSpecG into a final robust partition. The results of computational experiments with real and artificial LFR networks demonstrated a significant improvement in the results and performance of the introduced method in regard to another bi-objective algorithm found in the literature