An ensemble based on a bi-objective evolutionary spectral algorithm for graph clustering

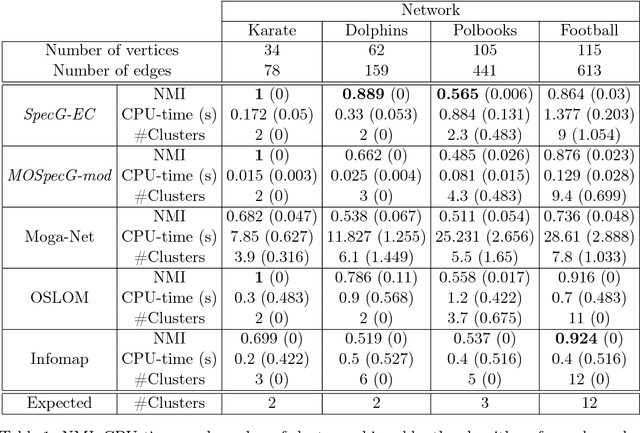
Graph clustering is a challenging pattern recognition problem whose goal is to identify vertex partitions with high intra-group connectivity. Because of the rough definition of this problem, there are numerous effective ways to formally determine such partitions. In particular, multi-objective optimization can deal with the trade-offs between different clustering quality measures in order to better assess the partitions. This paper investigates a problem that maximizes the number of intra-cluster edges of a graph and minimizes the expected number of inter-cluster edges in a random graph with the same degree sequence as the original one. The difference between the two investigated objectives is the definition of the well-known measure of graph clustering quality: the modularity. We introduce a spectral decomposition hybridized with an evolutionary heuristic, called MOSpecG, to approach this bi-objective problem and an ensemble strategy to consolidate the solutions found by MOSpecG into a final robust partition. The results of computational experiments with real and artificial LFR networks demonstrated a significant improvement in the results and performance of the introduced method in regard to another bi-objective algorithm found in the literature