DCT Approximations Based on Chen's Factorization

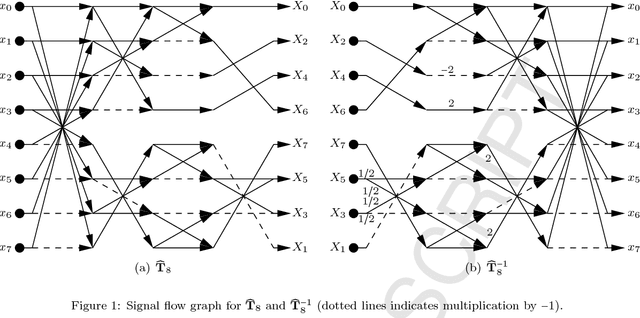
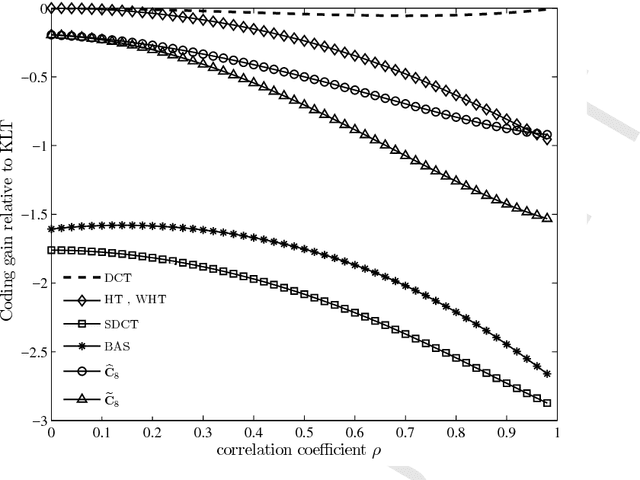
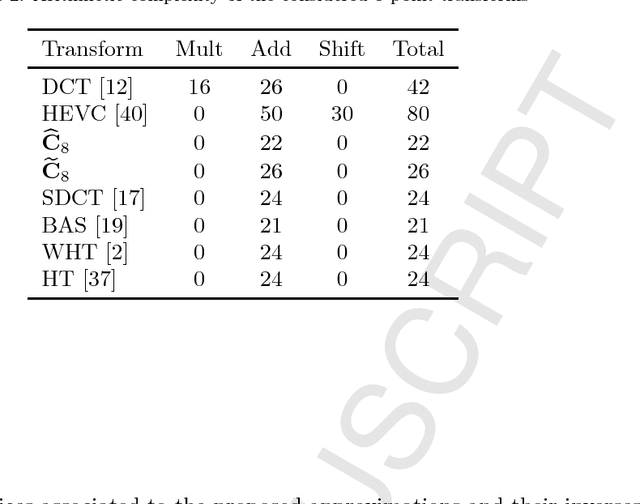
In this paper, two 8-point multiplication-free DCT approximations based on the Chen's factorization are proposed and their fast algorithms are also derived. Both transformations are assessed in terms of computational cost, error energy, and coding gain. Experiments with a JPEG-like image compression scheme are performed and results are compared with competing methods. The proposed low-complexity transforms are scaled according to Jridi-Alfalou-Meher algorithm to effect 16- and 32-point approximations. The new sets of transformations are embedded into an HEVC reference software to provide a fully HEVC-compliant video coding scheme. We show that approximate transforms can outperform traditional transforms and state-of-the-art methods at a very low complexity cost.

A Class of DCT Approximations Based on the Feig-Winograd Algorithm

A new class of matrices based on a parametrization of the Feig-Winograd factorization of 8-point DCT is proposed. Such parametrization induces a matrix subspace, which unifies a number of existing methods for DCT approximation. By solving a comprehensive multicriteria optimization problem, we identified several new DCT approximations. Obtained solutions were sought to possess the following properties: (i) low multiplierless computational complexity, (ii) orthogonality or near orthogonality, (iii) low complexity invertibility, and (iv) close proximity and performance to the exact DCT. Proposed approximations were submitted to assessment in terms of proximity to the DCT, coding performance, and suitability for image compression. Considering Pareto efficiency, particular new proposed approximations could outperform various existing methods archived in literature.