Burak Cevat Civek
Bayesian Sparse Blind Deconvolution Using MCMC Methods Based on Normal-Inverse-Gamma Prior
Aug 27, 2021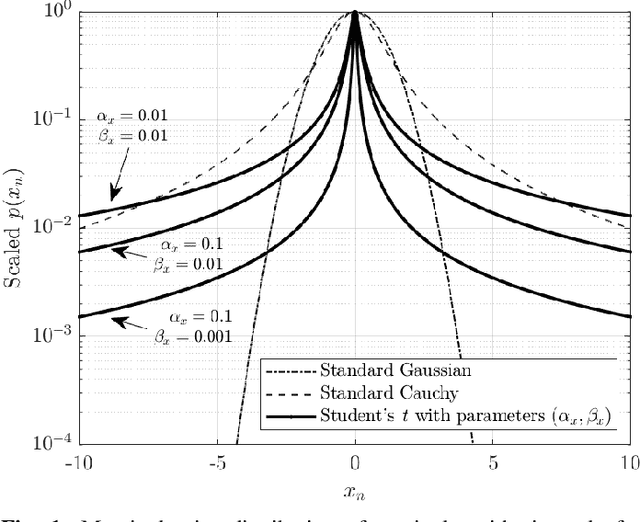
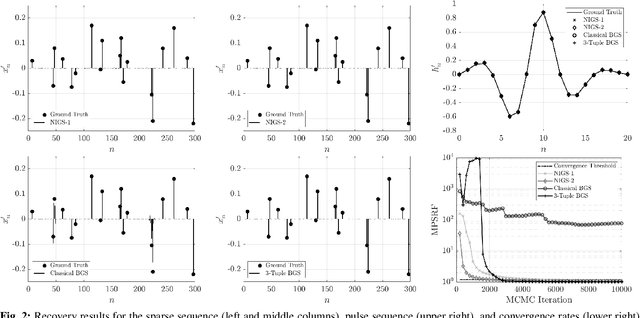
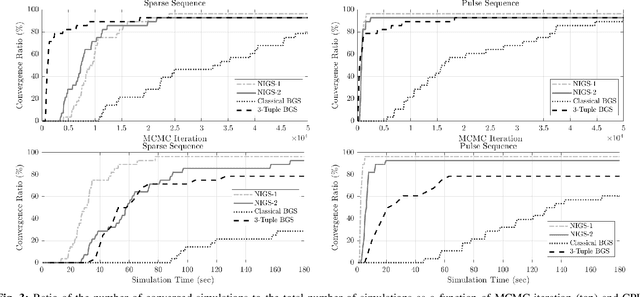
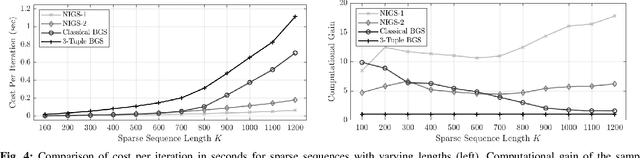
Abstract:Bayesian estimation methods for sparse blind deconvolution problems conventionally employ Bernoulli-Gaussian (BG) prior for modeling sparse sequences and utilize Markov Chain Monte Carlo (MCMC) methods for the estimation of unknowns. However, the discrete nature of the BG model creates computational bottlenecks, preventing efficient exploration of the probability space even with the recently proposed enhanced sampler schemes. To address this issue, we propose an alternative MCMC method by modeling the sparse sequences using the Normal-Inverse-Gamma (NIG) prior. We derive effective Gibbs samplers for this prior and illustrate that the computational burden associated with the BG model can be eliminated by transferring the problem into a completely continuous-valued framework. In addition to sparsity, we also incorporate time and frequency domain constraints on the convolving sequences. We demonstrate the effectiveness of the proposed methods via extensive simulations and characterize computational gains relative to the existing methods that utilize BG modeling.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge