Bugra Caskurlu
Multilevel Memetic Hypergraph Partitioning with Greedy Recombination
Apr 07, 2022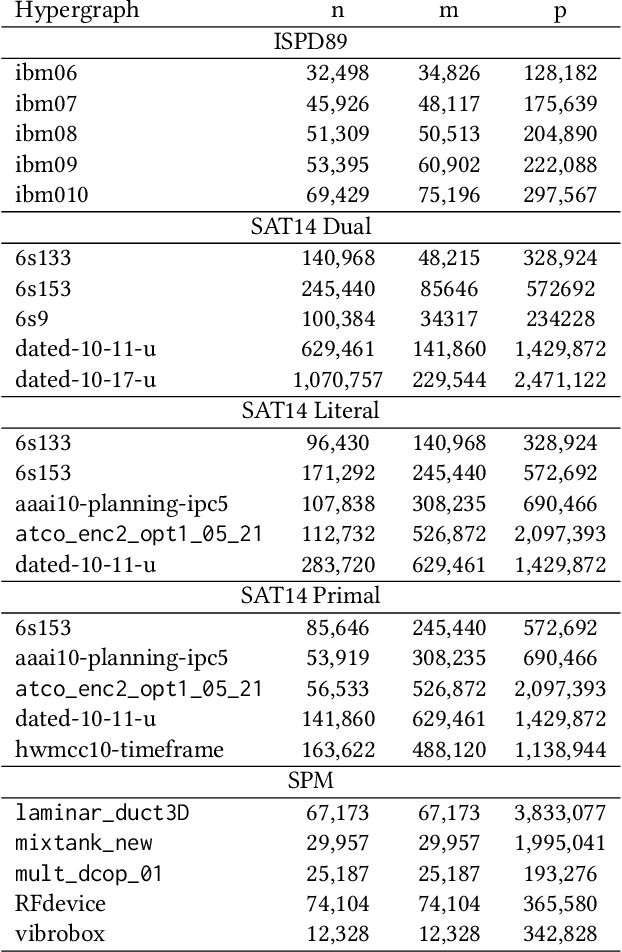
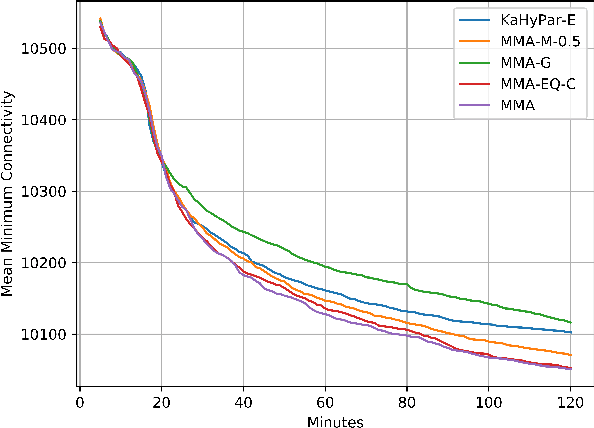
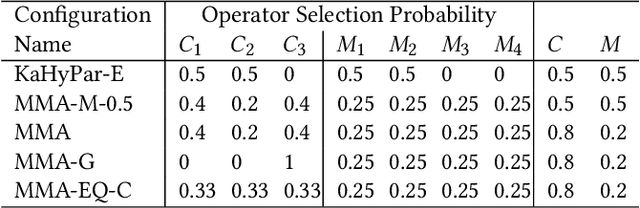
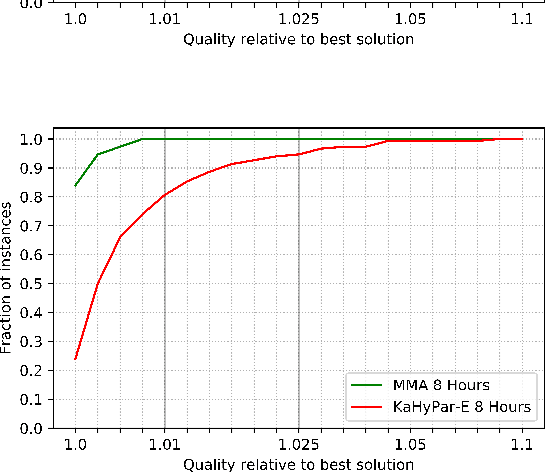
Abstract:The Hypergraph Partitioning (HGP) problem is a well-studied problem that finds applications in a variety of domains. The literature on the HGP problem has heavily focused on developing fast heuristic approaches. In several application domains, such as the VLSI design and database migration planning, the quality of the solution is more of a concern than the running time of the algorithm. KaHyPar-E is the first multilevel memetic algorithm designed for the HGP problem and it returns better quality solutions, compared to the heuristic algorithms, if sufficient computation time is given. In this work, we introduce novel problem-specific recombination and mutation operators, and develop a new multilevel memetic algorithm by combining KaHyPar-E with these operators. The performance of our algorithm is compared with the state-of-the-art HGP algorithms on $150$ real-life instances taken from the benchmark datasets used in the literature. In the experiments, which would take $39,000$ hours in a single-core computer, each algorithm is given $2, 4$, and $8$ hours to compute a solution for each instance. Our algorithm outperforms all others and finds the best solutions in $112$, $115$, and $125$ instances in $2, 4$, and $8$ hours, respectively.
On Singleton Congestion Games with Resilience Against Collusion
Nov 03, 2020
Abstract:We study the subclass of singleton congestion games with identical and increasing cost functions, i.e., each agent tries to utilize from the least crowded resource in her accessible subset of resources. Our main contribution is a novel approach for proving the existence of equilibrium outcomes that are resilient to weakly improving deviations: $(i)$ by singletons (Nash equilibria), $(ii)$ by the grand coalition (Pareto efficiency), and $(iii)$ by coalitions with respect to an a priori given partition coalition structure (partition equilibria). To the best of our knowledge, this is the strongest existence guarantee in the literature of congestion games that is resilient to weakly improving deviations by coalitions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge