Hierarchical Embedded Bayesian Additive Regression Trees

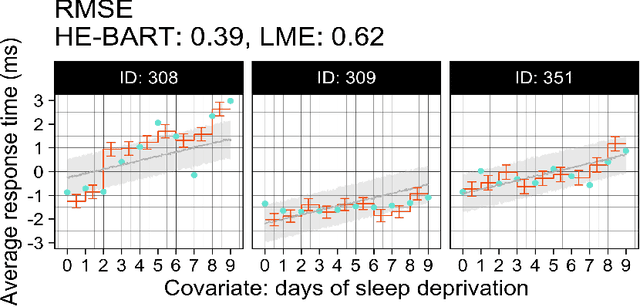
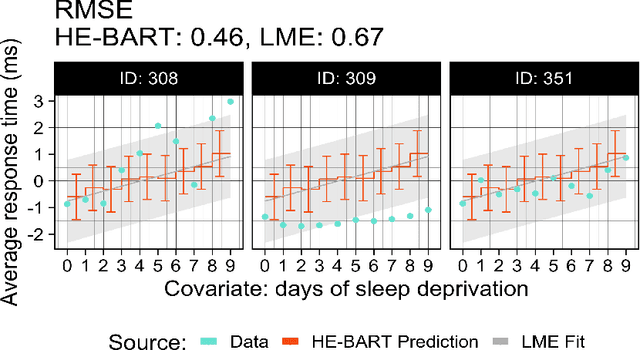
We propose a simple yet powerful extension of Bayesian Additive Regression Trees which we name Hierarchical Embedded BART (HE-BART). The model allows for random effects to be included at the terminal node level of a set of regression trees, making HE-BART a non-parametric alternative to mixed effects models which avoids the need for the user to specify the structure of the random effects in the model, whilst maintaining the prediction and uncertainty calibration properties of standard BART. Using simulated and real-world examples, we demonstrate that this new extension yields superior predictions for many of the standard mixed effects models' example data sets, and yet still provides consistent estimates of the random effect variances. In a future version of this paper, we outline its use in larger, more advanced data sets and structures.

Generalizing Gain Penalization for Feature Selection in Tree-based Models

We develop a new approach for feature selection via gain penalization in tree-based models. First, we show that previous methods do not perform sufficient regularization and often exhibit sub-optimal out-of-sample performance, especially when correlated features are present. Instead, we develop a new gain penalization idea that exhibits a general local-global regularization for tree-based models. The new method allows for more flexibility in the choice of feature-specific importance weights. We validate our method on both simulated and real data and implement itas an extension of the popular R package ranger.