Bridget W Mahony
Interpretable factorization of clinical questionnaires to identify latent factors of psychopathology
Dec 12, 2023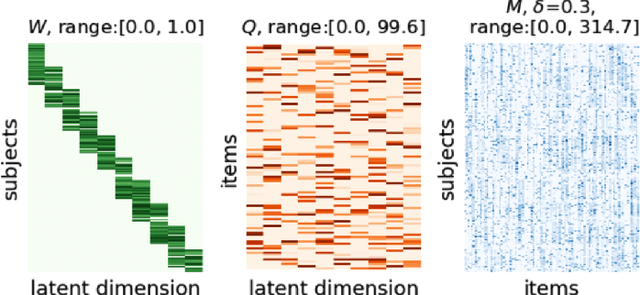
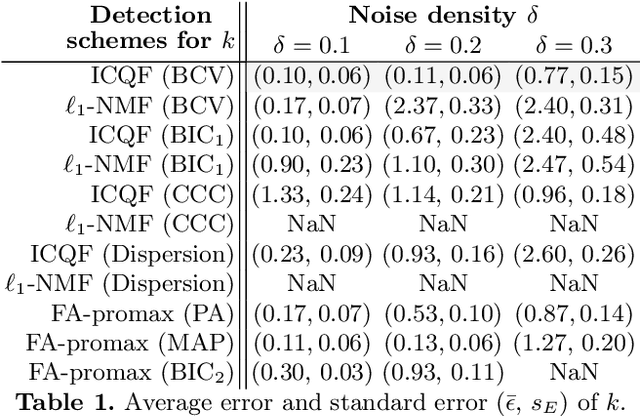
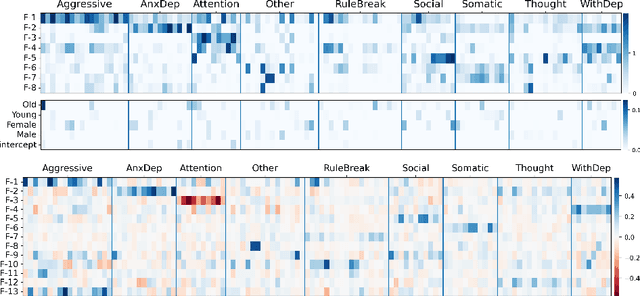
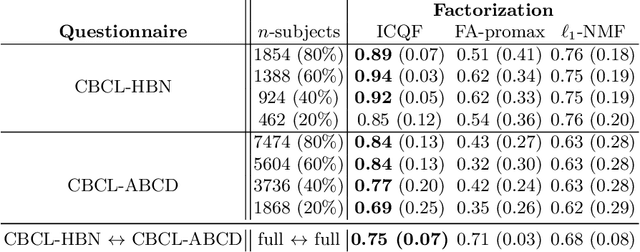
Abstract:Psychiatry research seeks to understand the manifestations of psychopathology in behavior, as measured in questionnaire data, by identifying a small number of latent factors that explain them. While factor analysis is the traditional tool for this purpose, the resulting factors may not be interpretable, and may also be subject to confounding variables. Moreover, missing data are common, and explicit imputation is often required. To overcome these limitations, we introduce interpretability constrained questionnaire factorization (ICQF), a non-negative matrix factorization method with regularization tailored for questionnaire data. Our method aims to promote factor interpretability and solution stability. We provide an optimization procedure with theoretical convergence guarantees, and an automated procedure to detect latent dimensionality accurately. We validate these procedures using realistic synthetic data. We demonstrate the effectiveness of our method in a widely used general-purpose questionnaire, in two independent datasets (the Healthy Brain Network and Adolescent Brain Cognitive Development studies). Specifically, we show that ICQF improves interpretability, as defined by domain experts, while preserving diagnostic information across a range of disorders, and outperforms competing methods for smaller dataset sizes. This suggests that the regularization in our method matches domain characteristics. The python implementation for ICQF is available at \url{https://github.com/jefferykclam/ICQF}.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge