Stability Via Adversarial Training of Neural Network Stochastic Control of Mean-Field Type

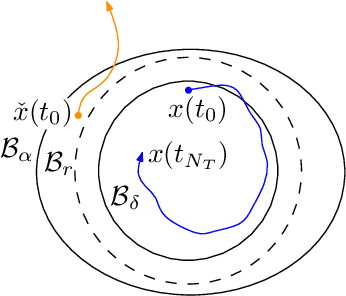
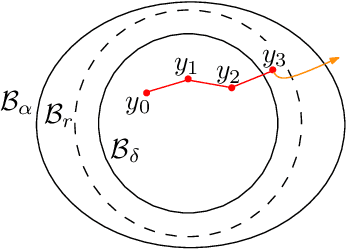
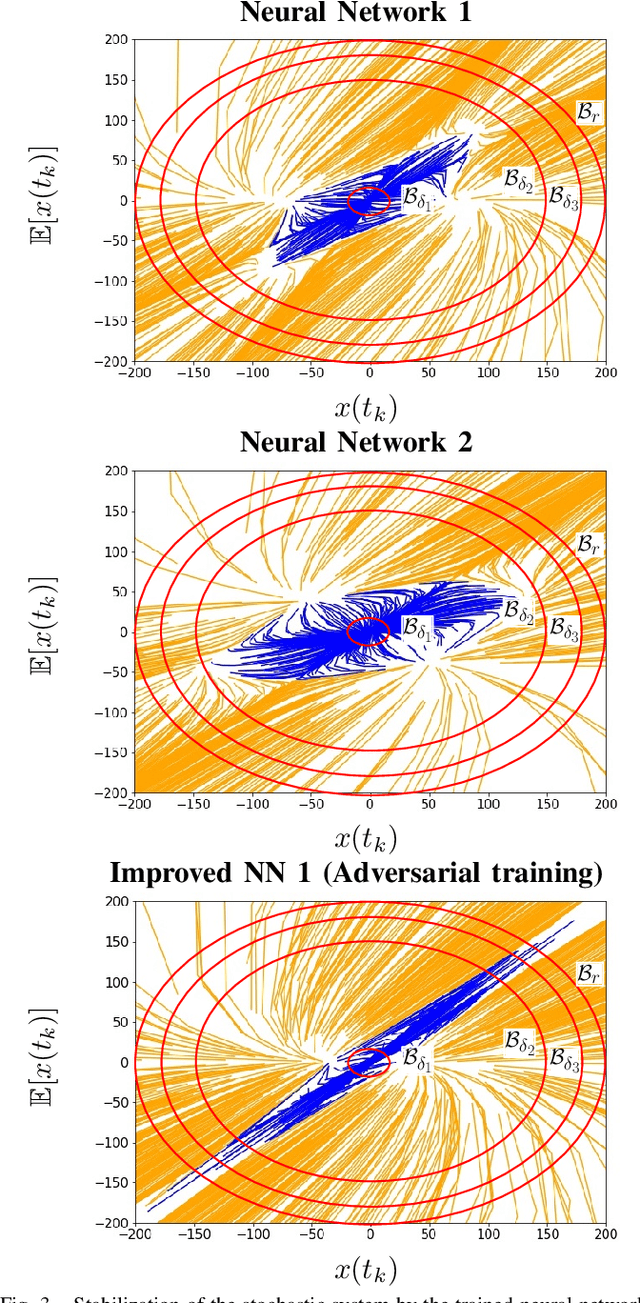
In this paper, we present an approach to neural network mean-field-type control and its stochastic stability analysis by means of adversarial inputs (aka adversarial attacks). This is a class of data-driven mean-field-type control where the distribution of the variables such as the system states and control inputs are incorporated into the problem. Besides, we present a methodology to validate the feasibility of the approximations of the solutions via neural networks and evaluate their stability. Moreover, we enhance the stability by enlarging the training set with adversarial inputs to obtain a more robust neural network. Finally, a worked-out example based on the linear-quadratic mean-field type control problem (LQ-MTC) is presented to illustrate our methodology.

Efficient learning of hidden state LTI state space models of unknown order

The aim of this paper is to address two related estimation problems arising in the setup of hidden state linear time invariant (LTI) state space systems when the dimension of the hidden state is unknown. Namely, the estimation of any finite number of the system's Markov parameters and the estimation of a minimal realization for the system, both from the partial observation of a single trajectory. For both problems, we provide statistical guarantees in the form of various estimation error upper bounds, $\rank$ recovery conditions, and sample complexity estimates. Specifically, we first show that the low $\rank$ solution of the Hankel penalized least square estimator satisfies an estimation error in $S_p$-norms for $p \in [1,2]$ that captures the effect of the system order better than the existing operator norm upper bound for the simple least square. We then provide a stability analysis for an estimation procedure based on a variant of the Ho-Kalman algorithm that improves both the dependence on the dimension and the least singular value of the Hankel matrix of the Markov parameters. Finally, we propose an estimation algorithm for the minimal realization that uses both the Hankel penalized least square estimator and the Ho-Kalman based estimation procedure and guarantees with high probability that we recover the correct order of the system and satisfies a new fast rate in the $S_2$-norm with a polynomial reduction in the dependence on the dimension and other parameters of the problem.

Non asymptotic estimation lower bounds for LTI state space models with Cramér-Rao and van Trees

We study the estimation problem for linear time-invariant (LTI) state-space models with Gaussian excitation of an unknown covariance. We provide non asymptotic lower bounds for the expected estimation error and the mean square estimation risk of the least square estimator, and the minimax mean square estimation risk. These bounds are sharp with explicit constants when the matrix of the dynamics has no eigenvalues on the unit circle and are rate-optimal when they do. Our results extend and improve existing lower bounds to lower bounds in expectation of the mean square estimation risk and to systems with a general noise covariance. Instrumental to our derivation are new concentration results for rescaled sample covariances and deviation results for the corresponding multiplication processes of the covariates, a differential geometric construction of a prior on the unit operator ball of small Fisher information, and an extension of the Cram\'er-Rao and van Treesinequalities to matrix-valued estimators.