Identification of Latent Variables From Graphical Model Residuals

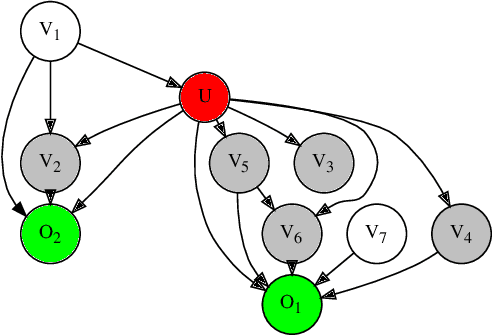
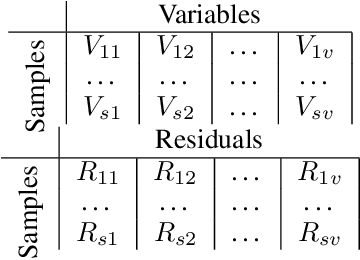
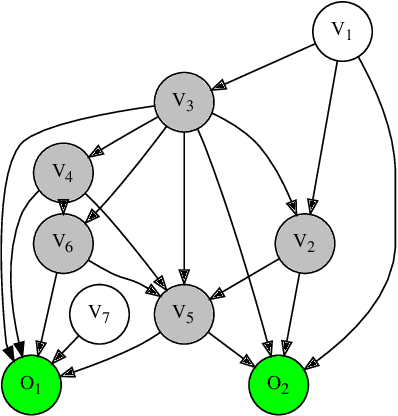
Graph-based causal discovery methods aim to capture conditional independencies consistent with the observed data and differentiate causal relationships from indirect or induced ones. Successful construction of graphical models of data depends on the assumption of causal sufficiency: that is, that all confounding variables are measured. When this assumption is not met, learned graphical structures may become arbitrarily incorrect and effects implied by such models may be wrongly attributed, carry the wrong magnitude, or mis-represent direction of correlation. Wide application of graphical models to increasingly less curated "big data" draws renewed attention to the unobserved confounder problem. We present a novel method that aims to control for the latent space when estimating a DAG by iteratively deriving proxies for the latent space from the residuals of the inferred model. Under mild assumptions, our method improves structural inference of Gaussian graphical models and enhances identifiability of the causal effect. In addition, when the model is being used to predict outcomes, it un-confounds the coefficients on the parents of the outcomes and leads to improved predictive performance when out-of-sample regime is very different from the training data. We show that any improvement of prediction of an outcome is intrinsically capped and cannot rise beyond a certain limit as compared to the confounded model. We extend our methodology beyond GGMs to ordinal variables and nonlinear cases. Our R package provides both PCA and autoencoder implementations of the methodology, suitable for GGMs with some guarantees and for better performance in general cases but without such guarantees.

MDL-motivated compression of GLM ensembles increases interpretability and retains predictive power

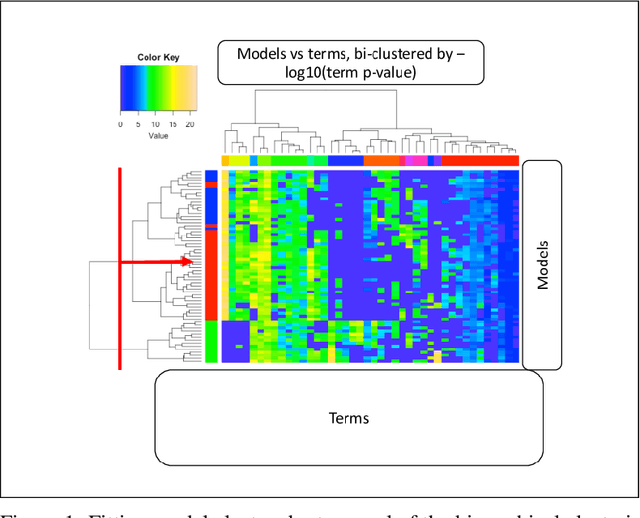
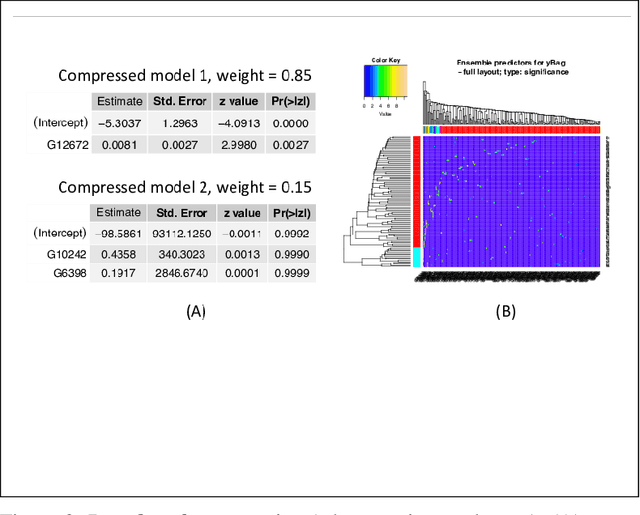
Over the years, ensemble methods have become a staple of machine learning. Similarly, generalized linear models (GLMs) have become very popular for a wide variety of statistical inference tasks. The former have been shown to enhance out- of-sample predictive power and the latter possess easy interpretability. Recently, ensembles of GLMs have been proposed as a possibility. On the downside, this approach loses the interpretability that GLMs possess. We show that minimum description length (MDL)-motivated compression of the inferred ensembles can be used to recover interpretability without much, if any, downside to performance and illustrate on a number of standard classification data sets.