MAGE: Human-Like Macro Placement via Agentic Multimodal Reasoning

Macro placement still requires substantial manual refinement in industrial physical design flows. We present MAGE (Macro Placement Agentic Engine), a multimodal multi-agent framework for macro placement refinement. MAGE decomposes the macro placement task into a six-phase workflow that combines structured floorplanning rules, visual checks, and iterative refinement. Expert floorplanning knowledge is encoded through natural-language directives and validation criteria, rather than learned from labeled placement data. A tournament-style refinement mode evaluates multiple candidate placements and propagates feedback from higher-quality solutions. We also introduce four metrics for quantifying human-likeness in macro placement: notch score, whitespace score, pocket score, and alignment score. These metrics capture structural properties used by expert designers but not directly measured by conventional PPA metrics. Across nine designs in NanGate45 and GlobalFoundries 12nm enablements, MAGE achieves geometric-mean improvements of 11.1%-19.3% in WNS and 70.0%-74.0% in TNS over commercial macro placers. On the three NanGate45 designs, for which human-expert and Hier-RTLMP baselines are available, MAGE improves WNS and TNS by 18.3% and 72.5% over the human expert, and by 47.0% and 80.4% over Hier-RTLMP, with comparable wirelength and power. On human-likeness metrics, MAGE improves the overall score by 6%-48% over all baselines. Additional case studies on anonymized netlists, unseen designs, dense rectilinear floorplans, and high-utilization settings show that the framework transfers to new placement settings without design-specific retraining.

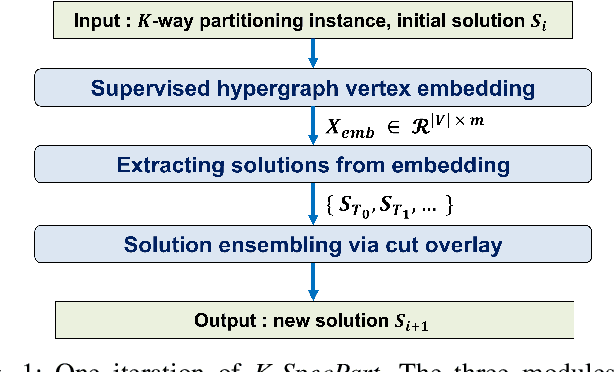
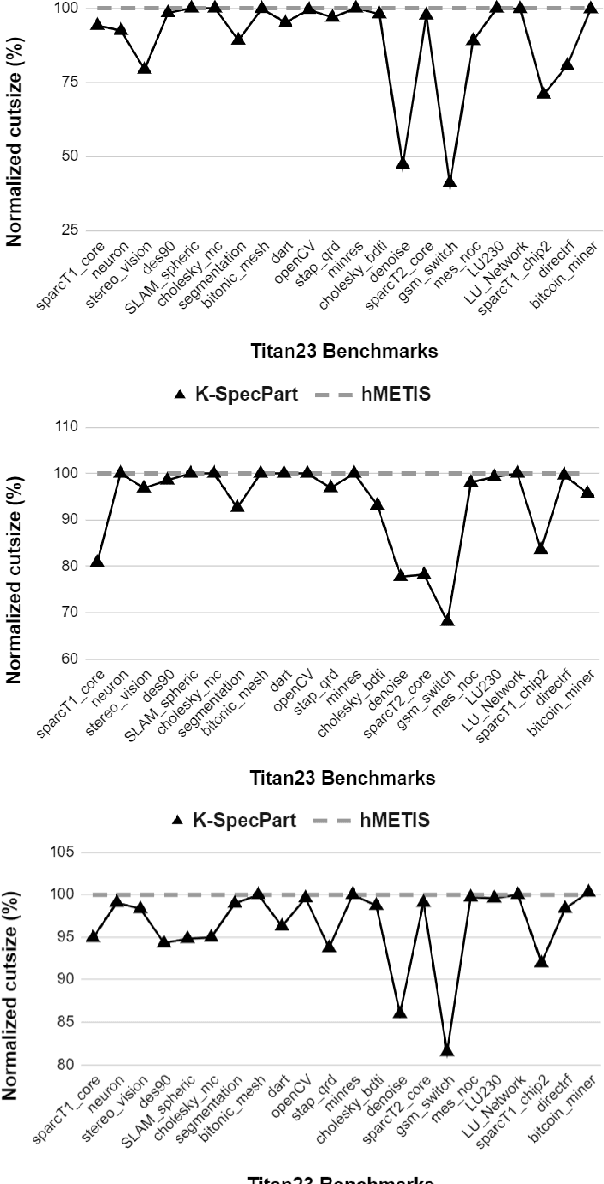
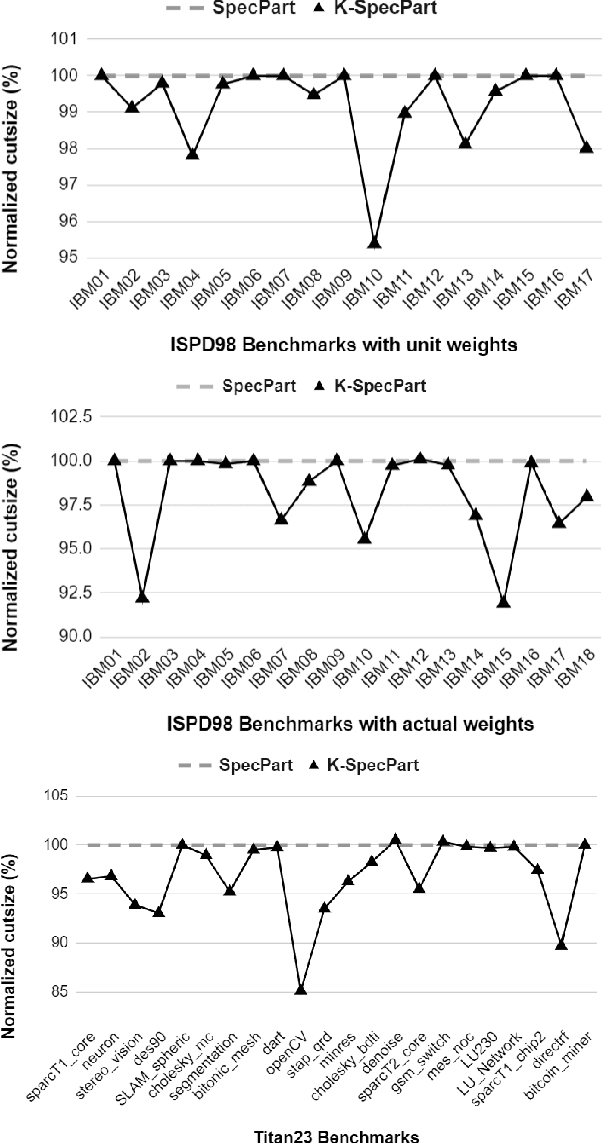
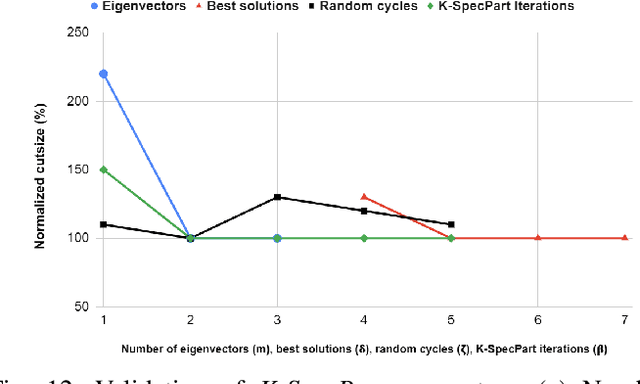
K-SpecPart: A Supervised Spectral Framework for Multi-Way Hypergraph Partitioning Solution Improvement

State-of-the-art hypergraph partitioners follow the multilevel paradigm, constructing multiple levels of coarser hypergraphs to drive cutsize refinement. These partitioners face limitations: (i) coarsening processes depend on local neighborhood structure, ignoring global hypergraph structure; (ii) refinement heuristics risk entrapment in local minima. We introduce K-SpecPart, a supervised spectral framework addressing these limitations by solving a generalized eigenvalue problem, capturing balanced partitioning objectives and global hypergraph structure in a low-dimensional vertex embedding while leveraging high-quality multilevel partitioning solutions as hints. In multi-way partitioning, K-SpecPart derives multiple bipartitioning solutions from a multi-way hint partitioning solution. It integrates these solutions into the generalized eigenvalue problem to compute eigenvectors, creating a large-dimensional embedding. Linear Discriminant Analysis (LDA) is used to transform this into a lower-dimensional embedding. K-SpecPart constructs a family of trees from the vertex embedding and partitions them using a tree-sweeping algorithm. We extend SpecPart's tree partitioning algorithm for multi-way partitioning. The multiple tree-based partitioning solutions are overlaid, followed by lifting to a clustered hypergraph where an integer linear programming (ILP) partitioning problem is solved. Empirical studies show K-SpecPart's benefits. For bipartitioning, K-SpecPart outperforms SpecPart with improvements up to 30%. For multi-way partitioning, K-SpecPart surpasses hMETIS and KaHyPar, with improvements up to 20% in some cases.