The Power of Typed Affine Decision Structures: A Case Study

TADS are a novel, concise white-box representation of neural networks. In this paper, we apply TADS to the problem of neural network verification, using them to generate either proofs or concise error characterizations for desirable neural network properties. In a case study, we consider the robustness of neural networks to adversarial attacks, i.e., small changes to an input that drastically change a neural networks perception, and show that TADS can be used to provide precise diagnostics on how and where robustness errors a occur. We achieve these results by introducing Precondition Projection, a technique that yields a TADS describing network behavior precisely on a given subset of its input space, and combining it with PCA, a traditional, well-understood dimensionality reduction technique. We show that PCA is easily compatible with TADS. All analyses can be implemented in a straightforward fashion using the rich algebraic properties of TADS, demonstrating the utility of the TADS framework for neural network explainability and verification. While TADS do not yet scale as efficiently as state-of-the-art neural network verifiers, we show that, using PCA-based simplifications, they can still scale to mediumsized problems and yield concise explanations for potential errors that can be used for other purposes such as debugging a network or generating new training samples.

Towards Rigorous Understanding of Neural Networks via Semantics-preserving Transformations

In this paper we present an algebraic approach to the precise and global verification and explanation of \emph{Rectifier Neural Networks}, a subclass of \emph{Piece-wise Linear Neural Networks} (PLNNs), i.e., networks that semantically represent piece-wise affine functions. Key to our approach is the symbolic execution of these networks that allows the construction of semantically equivalent \emph{Typed Affine Decision Structures} (TADS). Due to their deterministic and sequential nature, TADS can, similarly to decision trees, be considered as white-box models and therefore as precise solutions to the model and outcome explanation problem. TADS are linear algebras which allows one to elegantly compare Rectifier Networks for equivalence or similarity, both with precise diagnostic information in case of failure, and to characterize their classification potential by precisely characterizing the set of inputs that are specifically classified or the set of inputs where two network-based classifiers differ. All phenomena are illustrated along a detailed discussion of a minimal, illustrative example: the continuous XOR function.

ADD-Lib: Decision Diagrams in Practice

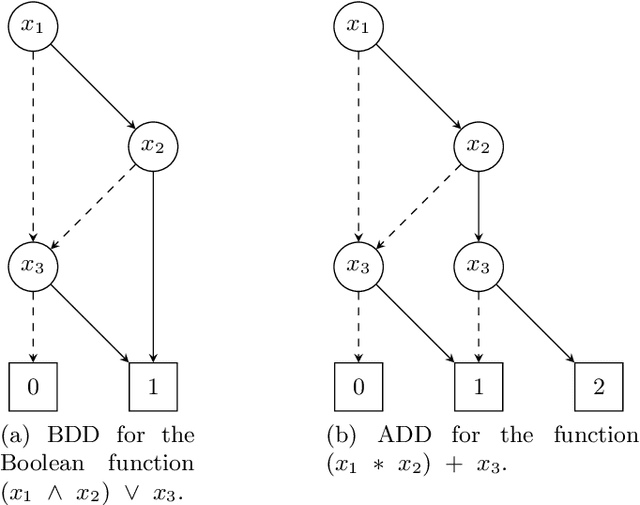
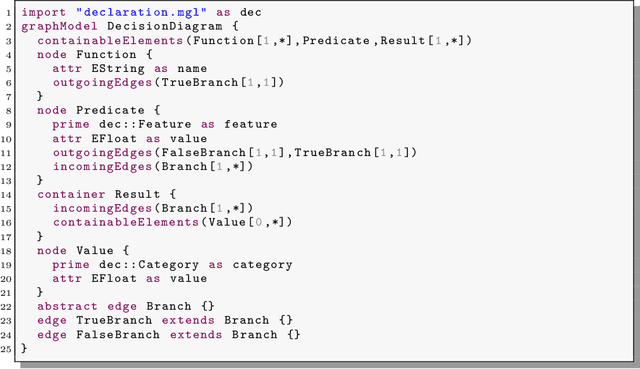
In the paper, we present the ADD-Lib, our efficient and easy to use framework for Algebraic Decision Diagrams (ADDs). The focus of the ADD-Lib is not so much on its efficient implementation of individual operations, which are taken by other established ADD frameworks, but its ease and flexibility, which arise at two levels: the level of individual ADD-tools, which come with a dedicated user-friendly web-based graphical user interface, and at the meta level, where such tools are specified. Both levels are described in the paper: the meta level by explaining how we can construct an ADD-tool tailored for Random Forest refinement and evaluation, and the accordingly generated Web-based domain-specific tool, which we also provide as an artifact for cooperative experimentation. In particular, the artifact allows readers to combine a given Random Forest with their own ADDs regarded as expert knowledge and to experience the corresponding effect.

Large Random Forests: Optimisation for Rapid Evaluation

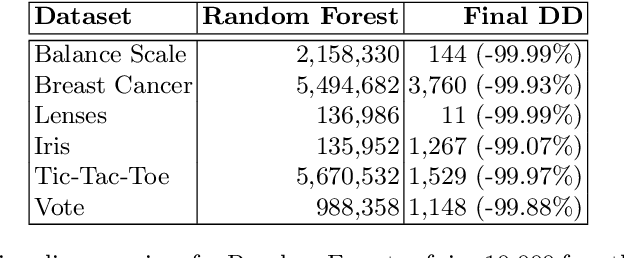
Random Forests are one of the most popular classifiers in machine learning. The larger they are, the more precise is the outcome of their predictions. However, this comes at a cost: their running time for classification grows linearly with the number of trees, i.e. the size of the forest. In this paper, we propose a method to aggregate large Random Forests into a single, semantically equivalent decision diagram. Our experiments on various popular datasets show speed-ups of several orders of magnitude, while, at the same time, also significantly reducing the size of the required data structure.