Deep Neural Networks for Encrypted Inference with TFHE

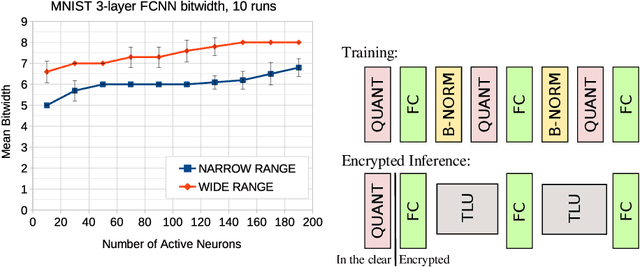
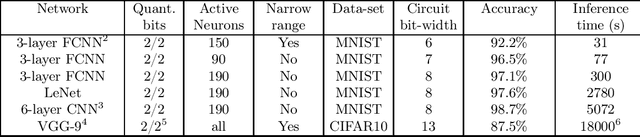
Fully homomorphic encryption (FHE) is an encryption method that allows to perform computation on encrypted data, without decryption. FHE preserves the privacy of the users of online services that handle sensitive data, such as health data, biometrics, credit scores and other personal information. A common way to provide a valuable service on such data is through machine learning and, at this time, Neural Networks are the dominant machine learning model for unstructured data. In this work we show how to construct Deep Neural Networks (DNN) that are compatible with the constraints of TFHE, an FHE scheme that allows arbitrary depth computation circuits. We discuss the constraints and show the architecture of DNNs for two computer vision tasks. We benchmark the architectures using the Concrete stack, an open-source implementation of TFHE.

Privacy-Preserving Tree-Based Inference with Fully Homomorphic Encryption

Privacy enhancing technologies (PETs) have been proposed as a way to protect the privacy of data while still allowing for data analysis. In this work, we focus on Fully Homomorphic Encryption (FHE), a powerful tool that allows for arbitrary computations to be performed on encrypted data. FHE has received lots of attention in the past few years and has reached realistic execution times and correctness. More precisely, we explain in this paper how we apply FHE to tree-based models and get state-of-the-art solutions over encrypted tabular data. We show that our method is applicable to a wide range of tree-based models, including decision trees, random forests, and gradient boosted trees, and has been implemented within the Concrete-ML library, which is open-source at https://github.com/zama-ai/concrete-ml. With a selected set of use-cases, we demonstrate that our FHE version is very close to the unprotected version in terms of accuracy.