Projection-Free Online Convex Optimization with Time-Varying Constraints

We consider the setting of online convex optimization with adversarial time-varying constraints in which actions must be feasible w.r.t. a fixed constraint set, and are also required on average to approximately satisfy additional time-varying constraints. Motivated by scenarios in which the fixed feasible set (hard constraint) is difficult to project on, we consider projection-free algorithms that access this set only through a linear optimization oracle (LOO). We present an algorithm that, on a sequence of length $T$ and using overall $T$ calls to the LOO, guarantees $\tilde{O}(T^{3/4})$ regret w.r.t. the losses and $O(T^{7/8})$ constraints violation (ignoring all quantities except for $T$) . In particular, these bounds hold w.r.t. any interval of the sequence. We also present a more efficient algorithm that requires only first-order oracle access to the soft constraints and achieves similar bounds w.r.t. the entire sequence. We extend the latter to the setting of bandit feedback and obtain similar bounds (as a function of $T$) in expectation.

Projection-free Online Exp-concave Optimization

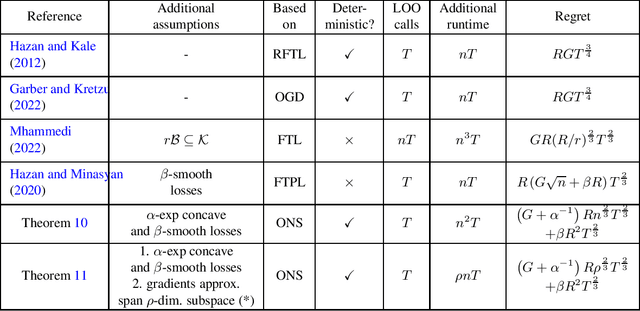
We consider the setting of online convex optimization (OCO) with \textit{exp-concave} losses. The best regret bound known for this setting is $O(n\log{}T)$, where $n$ is the dimension and $T$ is the number of prediction rounds (treating all other quantities as constants and assuming $T$ is sufficiently large), and is attainable via the well-known Online Newton Step algorithm (ONS). However, ONS requires on each iteration to compute a projection (according to some matrix-induced norm) onto the feasible convex set, which is often computationally prohibitive in high-dimensional settings and when the feasible set admits a non-trivial structure. In this work we consider projection-free online algorithms for exp-concave and smooth losses, where by projection-free we refer to algorithms that rely only on the availability of a linear optimization oracle (LOO) for the feasible set, which in many applications of interest admits much more efficient implementations than a projection oracle. We present an LOO-based ONS-style algorithm, which using overall $O(T)$ calls to a LOO, guarantees in worst case regret bounded by $\widetilde{O}(n^{2/3}T^{2/3})$ (ignoring all quantities except for $n,T$). However, our algorithm is most interesting in an important and plausible low-dimensional data scenario: if the gradients (approximately) span a subspace of dimension at most $\rho$, $\rho << n$, the regret bound improves to $\widetilde{O}(\rho^{2/3}T^{2/3})$, and by applying standard deterministic sketching techniques, both the space and average additional per-iteration runtime requirements are only $O(\rho{}n)$ (instead of $O(n^2)$). This improves upon recently proposed LOO-based algorithms for OCO which, while having the same state-of-the-art dependence on the horizon $T$, suffer from regret/oracle complexity that scales with $\sqrt{n}$ or worse.

New Projection-free Algorithms for Online Convex Optimization with Adaptive Regret Guarantees

We present new efficient \textit{projection-free} algorithms for online convex optimization (OCO), where by projection-free we refer to algorithms that avoid computing orthogonal projections onto the feasible set, and instead relay on different and potentially much more efficient oracles. While most state-of-the-art projection-free algorithms are based on the \textit{follow-the-leader} framework, our algorithms are fundamentally different and are based on the \textit{online gradient descent} algorithm with a novel and efficient approach to computing so-called \textit{infeasible projections}. As a consequence, we obtain the first projection-free algorithms which naturally yield \textit{adaptive regret} guarantees, i.e., regret bounds that hold w.r.t. any sub-interval of the sequence. Concretely, when assuming the availability of a linear optimization oracle (LOO) for the feasible set, on a sequence of length $T$, our algorithms guarantee $O(T^{3/4})$ adaptive regret and $O(T^{3/4})$ adaptive expected regret, for the full-information and bandit settings, respectively, using only $O(T)$ calls to the LOO. These bounds match the current state-of-the-art regret bounds for LOO-based projection-free OCO, which are \textit{not adaptive}. We also consider a new natural setting in which the feasible set is accessible through a separation oracle. We present algorithms which, using overall $O(T)$ calls to the separation oracle, guarantee $O(\sqrt{T})$ adaptive regret and $O(T^{3/4})$ adaptive expected regret for the full-information and bandit settings, respectively.

Revisiting Projection-free Online Learning: the Strongly Convex Case

Projection-free optimization algorithms, which are mostly based on the classical Frank-Wolfe method, have gained significant interest in the machine learning community in recent years due to their ability to handle convex constraints that are popular in many applications, but for which computing projections is often computationally impractical in high-dimensional settings, and hence prohibit the use of most standard projection-based methods. In particular, a significant research effort was put on projection-free methods for online learning. In this paper we revisit the Online Frank-Wolfe (OFW) method suggested by Hazan and Kale \cite{Hazan12} and fill a gap that has been left unnoticed for several years: OFW achieves a faster rate of $O(T^{2/3})$ on strongly convex functions (as opposed to the standard $O(T^{3/4})$ for convex but not strongly convex functions), where $T$ is the sequence length. This is somewhat surprising since it is known that for offline optimization, in general, strong convexity does not lead to faster rates for Frank-Wolfe. We also revisit the bandit setting under strong convexity and prove a similar bound of $\tilde O(T^{2/3})$ (instead of $O(T^{3/4})$ without strong convexity). Hence, in the current state-of-affairs, the best projection-free upper-bounds for the full-information and bandit settings with strongly convex and nonsmooth functions match, up to logarithmic factors, in $T$.

Improved Regret Bounds for Projection-free Bandit Convex Optimization

We revisit the challenge of designing online algorithms for the bandit convex optimization problem (BCO) which are also scalable to high dimensional problems. Hence, we consider algorithms that are \textit{projection-free}, i.e., based on the conditional gradient method whose only access to the feasible decision set, is through a linear optimization oracle (as opposed to other methods which require potentially much more computationally-expensive subprocedures, such as computing Euclidean projections). We present the first such algorithm that attains $O(T^{3/4})$ expected regret using only $O(T)$ overall calls to the linear optimization oracle, in expectation, where $T$ is the number of prediction rounds. This improves over the $O(T^{4/5})$ expected regret bound recently obtained by \cite{Karbasi19}, and actually matches the current best regret bound for projection-free online learning in the \textit{full information} setting.