Tiny Learning-Based MPC for Multirotors: Solver-Aware Learning for Efficient Embedded Predictive Control

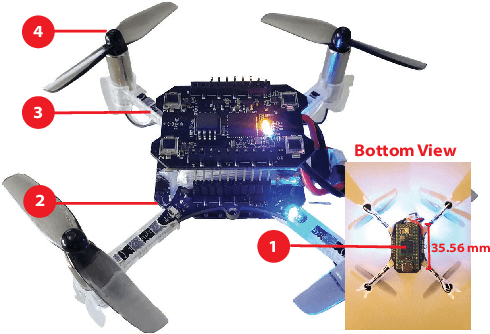
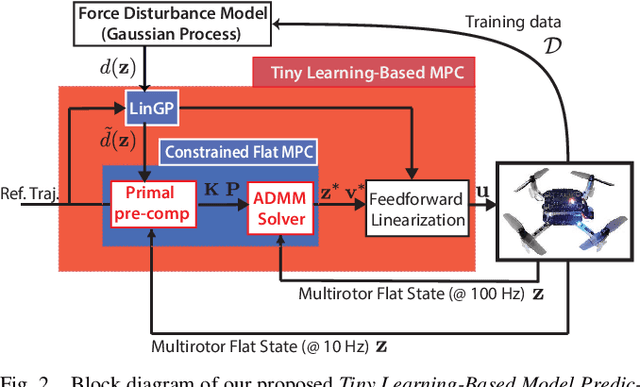
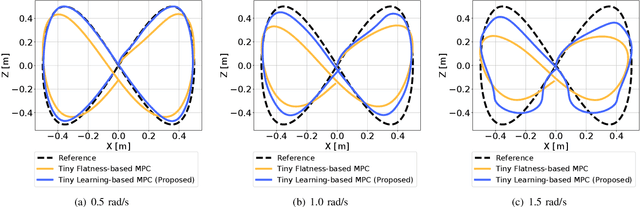
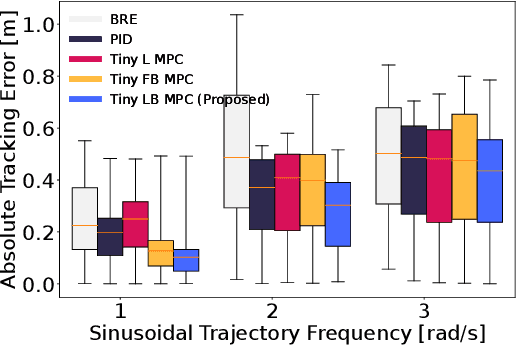
Tiny aerial robots show promise for applications like environmental monitoring and search-and-rescue but face challenges in control due to their limited computing power and complex dynamics. Model Predictive Control (MPC) can achieve agile trajectory tracking and handle constraints. Although current learning-based MPC methods, such as Gaussian Process (GP) MPC, improve control performance by learning residual dynamics, they are computationally demanding, limiting their onboard application on tiny robots. This paper introduces Tiny Learning-Based Model Predictive Control (LB MPC), a novel framework for resource-constrained micro multirotor platforms. By exploiting multirotor dynamics' structure and developing an efficient solver, our approach enables high-rate control at 100 Hz on a Crazyflie 2.1 with a Teensy 4.0 microcontroller. We demonstrate a 23\% average improvement in tracking performance over existing embedded MPC methods, achieving the first onboard implementation of learning-based MPC on a tiny multirotor (53 g).

A Computationally Efficient Learning-Based Model Predictive Control for Multirotors under Aerodynamic Disturbances

Neglecting complex aerodynamic effects hinders high-speed yet high-precision multirotor autonomy. In this paper, we present a computationally efficient learning-based model predictive controller that simultaneously optimizes a trajectory that can be tracked within the physical limits (on thrust and orientation) of the multirotor system despite unknown aerodynamic forces and adapts the control input. To do this, we leverage the well-known differential flatness property of multirotors, which allows us to transform their nonlinear dynamics into a linear model. The main limitation of current flatness-based planning and control approaches is that they often neglect dynamic feasibility. This is because these constraints are nonlinear as a result of the mapping between the input, i.e., multirotor thrust, and the flat state. In our approach, we learn a novel representation of the drag forces by learning the mapping from the flat state to the multirotor thrust vector (in a world frame) as a Gaussian Process (GP). Our proposed approach leverages the properties of GPs to develop a convex optimal controller that can be iteratively solved as a second-order cone program (SOCP). In simulation experiments, our proposed approach outperforms related model predictive controllers that do not account for aerodynamic effects on trajectory feasibility, leading to a reduction of up to 55% in absolute tracking error.