B. Rajesh Kanna
P-HGRMS: A Parallel Hypergraph Based Root Mean Square Algorithm for Image Denoising
Jun 29, 2013Abstract:This paper presents a parallel Salt and Pepper (SP) noise removal algorithm in a grey level digital image based on the Hypergraph Based Root Mean Square (HGRMS) approach. HGRMS is generic algorithm for identifying noisy pixels in any digital image using a two level hierarchical serial approach. However, for SP noise removal, we reduce this algorithm to a parallel model by introducing a cardinality matrix and an iteration factor, k, which helps us reduce the dependencies in the existing approach. We also observe that the performance of the serial implementation is better on smaller images, but once the threshold is achieved in terms of image resolution, its computational complexity increases drastically. We test P-HGRMS using standard images from the Berkeley Segmentation dataset on NVIDIAs Compute Unified Device Architecture (CUDA) for noise identification and attenuation. We also compare the noise removal efficiency of the proposed algorithm using Peak Signal to Noise Ratio (PSNR) to the existing approach. P-HGRMS maintains the noise removal efficiency and outperforms its sequential counterpart by 6 to 18 times (6x - 18x) in computational efficiency.
Exploiting Data Parallelism in the yConvex Hypergraph Algorithm for Image Representation using GPGPUs
Jun 23, 2013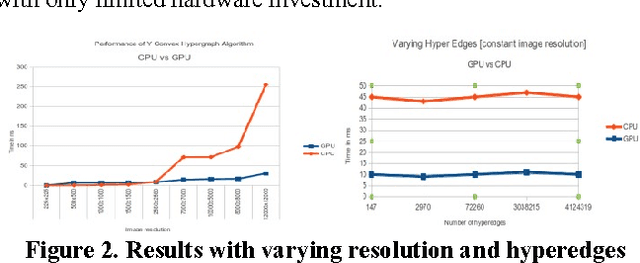
Abstract:To define and identify a region-of-interest (ROI) in a digital image, the shape descriptor of the ROI has to be described in terms of its boundary characteristics. To address the generic issues of contour tracking, the yConvex Hypergraph (yCHG) model was proposed by Kanna et al [1]. In this work, we propose a parallel approach to implement the yCHG model by exploiting massively parallel cores of NVIDIA's Compute Unified Device Architecture (CUDA). We perform our experiments on the MODIS satellite image database by NASA, and based on our analysis we observe that the performance of the serial implementation is better on smaller images, but once the threshold is achieved in terms of image resolution, the parallel implementation outperforms its sequential counterpart by 2 to 10 times (2x-10x). We also conclude that an increase in the number of hyperedges in the ROI of a given size does not impact the performance of the overall algorithm.
* 1 page, 1 figure published in Proceedings of the 27th ACM International Conference on Supercomputing, ICS 2013, Eugene, Oregon, USA
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge