Measuring Visual Complexity of Cluster-Based Visualizations

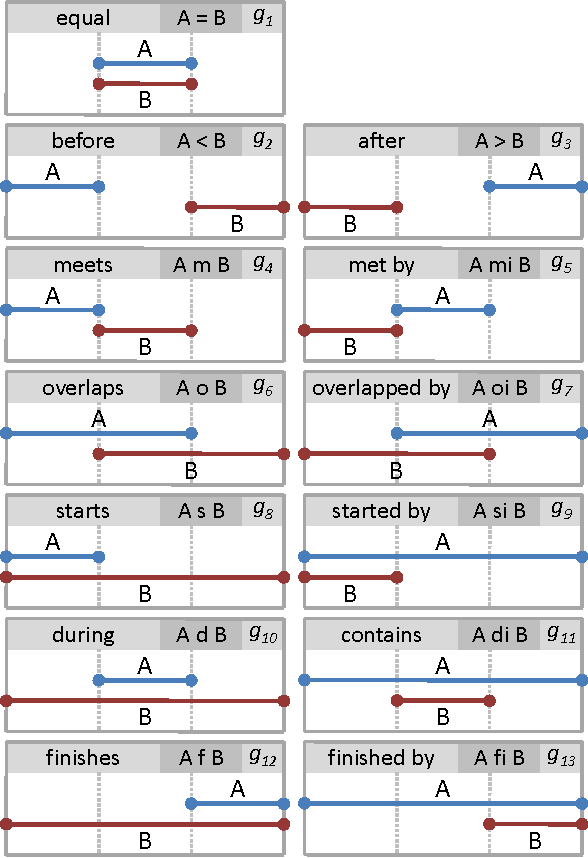
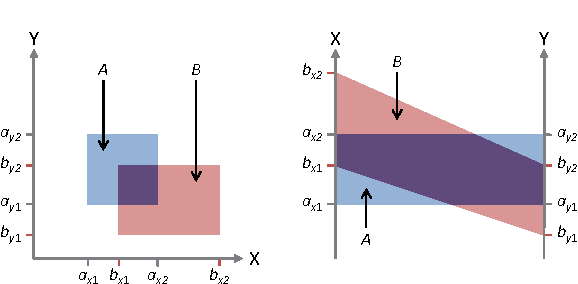
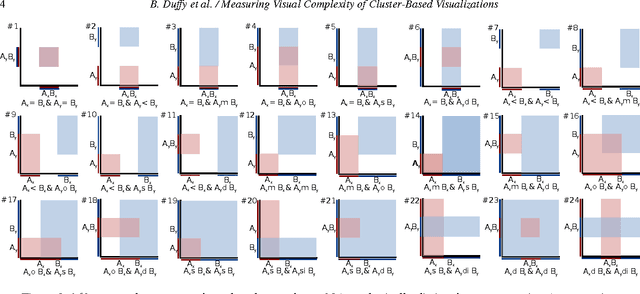
Handling visual complexity is a challenging problem in visualization owing to the subjectiveness of its definition and the difficulty in devising generalizable quantitative metrics. In this paper we address this challenge by measuring the visual complexity of two common forms of cluster-based visualizations: scatter plots and parallel coordinatess. We conceptualize visual complexity as a form of visual uncertainty, which is a measure of the degree of difficulty for humans to interpret a visual representation correctly. We propose an algorithm for estimating visual complexity for the aforementioned visualizations using Allen's interval algebra. We first establish a set of primitive 2-cluster cases in scatter plots and another set for parallel coordinatess based on symmetric isomorphism. We confirm that both are the minimal sets and verify the correctness of their members computationally. We score the uncertainty of each primitive case based on its topological properties, including the existence of overlapping regions, splitting regions and meeting points or edges. We compare a few optional scoring schemes against a set of subjective scores by humans, and identify the one that is the most consistent with the subjective scores. Finally, we extend the 2-cluster measure to k-cluster measure as a general purpose estimator of visual complexity for these two forms of cluster-based visualization.