A multilevel reinforcement learning framework for PDE based control

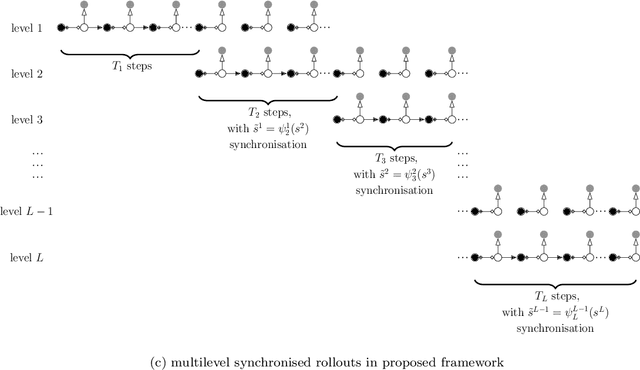
Reinforcement learning (RL) is a promising method to solve control problems. However, model-free RL algorithms are sample inefficient and require thousands if not millions of samples to learn optimal control policies. A major source of computational cost in RL corresponds to the transition function, which is dictated by the model dynamics. This is especially problematic when model dynamics is represented with coupled PDEs. In such cases, the transition function often involves solving a large-scale discretization of the said PDEs. We propose a multilevel RL framework in order to ease this cost by exploiting sublevel models that correspond to coarser scale discretization (i.e. multilevel models). This is done by formulating an approximate multilevel Monte Carlo estimate of the objective function of the policy and / or value network instead of Monte Carlo estimates, as done in the classical framework. As a demonstration of this framework, we present a multilevel version of the proximal policy optimization (PPO) algorithm. Here, the level refers to the grid fidelity of the chosen simulation-based environment. We provide two examples of simulation-based environments that employ stochastic PDEs that are solved using finite-volume discretization. For the case studies presented, we observed substantial computational savings using multilevel PPO compared to its classical counterpart.

Robust optimal well control using an adaptive multi-grid reinforcement learning framework

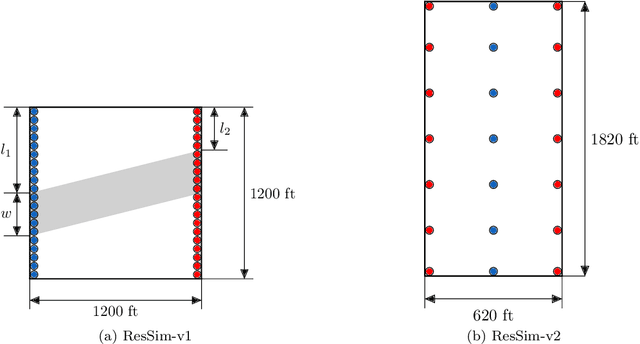
Reinforcement learning (RL) is a promising tool to solve robust optimal well control problems where the model parameters are highly uncertain, and the system is partially observable in practice. However, RL of robust control policies often relies on performing a large number of simulations. This could easily become computationally intractable for cases with computationally intensive simulations. To address this bottleneck, an adaptive multi-grid RL framework is introduced which is inspired by principles of geometric multi-grid methods used in iterative numerical algorithms. RL control policies are initially learned using computationally efficient low fidelity simulations using coarse grid discretization of the underlying partial differential equations (PDEs). Subsequently, the simulation fidelity is increased in an adaptive manner towards the highest fidelity simulation that correspond to finest discretization of the model domain. The proposed framework is demonstrated using a state-of-the-art, model-free policy-based RL algorithm, namely the Proximal Policy Optimisation (PPO) algorithm. Results are shown for two case studies of robust optimal well control problems which are inspired from SPE-10 model 2 benchmark case studies. Prominent gains in the computational efficiency is observed using the proposed framework saving around 60-70% of computational cost of its single fine-grid counterpart.

Stochastic optimal well control in subsurface reservoirs using reinforcement learning

We present a case study of model-free reinforcement learning (RL) framework to solve stochastic optimal control for a predefined parameter uncertainty distribution and partially observable system. We focus on robust optimal well control problem which is a subject of intensive research activities in the field of subsurface reservoir management. For this problem, the system is partially observed since the data is only available at well locations. Furthermore, the model parameters are highly uncertain due to sparsity of available field data. In principle, RL algorithms are capable of learning optimal action policies -- a map from states to actions -- to maximize a numerical reward signal. In deep RL, this mapping from state to action is parameterized using a deep neural network. In the RL formulation of the robust optimal well control problem, the states are represented by saturation and pressure values at well locations while the actions represent the valve openings controlling the flow through wells. The numerical reward refers to the total sweep efficiency and the uncertain model parameter is the subsurface permeability field. The model parameter uncertainties are handled by introducing a domain randomisation scheme that exploits cluster analysis on its uncertainty distribution. We present numerical results using two state-of-the-art RL algorithms, proximal policy optimization (PPO) and advantage actor-critic (A2C), on two subsurface flow test cases representing two distinct uncertainty distributions of permeability field. The results were benchmarked against optimisation results obtained using differential evolution algorithm. Furthermore, we demonstrate the robustness of the proposed use of RL by evaluating the learned control policy on unseen samples drawn from the parameter uncertainty distribution that were not used during the training process.