A multilevel reinforcement learning framework for PDE based control

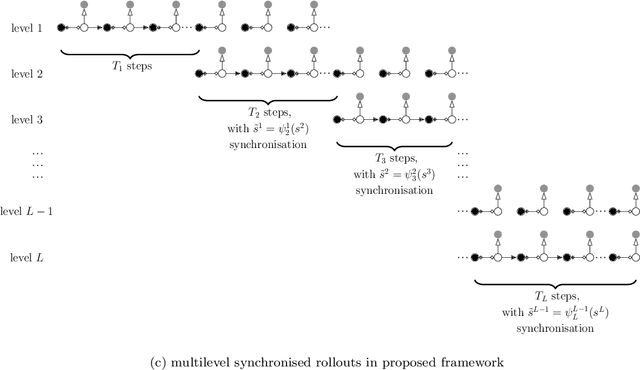
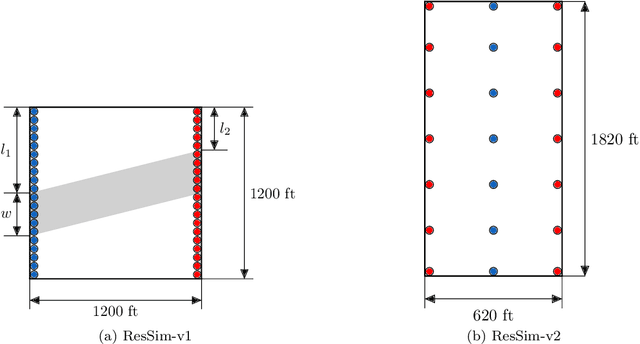
Reinforcement learning (RL) is a promising method to solve control problems. However, model-free RL algorithms are sample inefficient and require thousands if not millions of samples to learn optimal control policies. A major source of computational cost in RL corresponds to the transition function, which is dictated by the model dynamics. This is especially problematic when model dynamics is represented with coupled PDEs. In such cases, the transition function often involves solving a large-scale discretization of the said PDEs. We propose a multilevel RL framework in order to ease this cost by exploiting sublevel models that correspond to coarser scale discretization (i.e. multilevel models). This is done by formulating an approximate multilevel Monte Carlo estimate of the objective function of the policy and / or value network instead of Monte Carlo estimates, as done in the classical framework. As a demonstration of this framework, we present a multilevel version of the proximal policy optimization (PPO) algorithm. Here, the level refers to the grid fidelity of the chosen simulation-based environment. We provide two examples of simulation-based environments that employ stochastic PDEs that are solved using finite-volume discretization. For the case studies presented, we observed substantial computational savings using multilevel PPO compared to its classical counterpart.