Time-dependent density estimation using binary classifiers

We propose a data-driven method to learn the time-dependent probability density of a multivariate stochastic process from sample paths, assuming that the initial probability density is known and can be evaluated. Our method uses a novel time-dependent binary classifier trained using a contrastive estimation-based objective that trains the classifier to discriminate between realizations of the stochastic process at two nearby time instants. Significantly, the proposed method explicitly models the time-dependent probability distribution, which means that it is possible to obtain the value of the probability density within the time horizon of interest. Additionally, the input before the final activation in the time-dependent classifier is a second-order approximation to the partial derivative, with respect to time, of the logarithm of the density. We apply the proposed approach to approximate the time-dependent probability density functions for systems driven by stochastic excitations. We also use the proposed approach to synthesize new samples of a random vector from a given set of its realizations. In such applications, we generate sample paths necessary for training using stochastic interpolants. Subsequently, new samples are generated using gradient-based Markov chain Monte Carlo methods because automatic differentiation can efficiently provide the necessary gradient. Further, we demonstrate the utility of an explicit approximation to the time-dependent probability density function through applications in unsupervised outlier detection. Through several numerical experiments, we show that the proposed method accurately reconstructs complex time-dependent, multi-modal, and near-degenerate densities, scales effectively to moderately high-dimensional problems, and reliably detects rare events among real-world data.

Unifying and extending Diffusion Models through PDEs for solving Inverse Problems

Diffusion models have emerged as powerful generative tools with applications in computer vision and scientific machine learning (SciML), where they have been used to solve large-scale probabilistic inverse problems. Traditionally, these models have been derived using principles of variational inference, denoising, statistical signal processing, and stochastic differential equations. In contrast to the conventional presentation, in this study we derive diffusion models using ideas from linear partial differential equations and demonstrate that this approach has several benefits that include a constructive derivation of the forward and reverse processes, a unified derivation of multiple formulations and sampling strategies, and the discovery of a new class of models. We also apply the conditional version of these models to solving canonical conditional density estimation problems and challenging inverse problems. These problems help establish benchmarks for systematically quantifying the performance of different formulations and sampling strategies in this study, and for future studies. Finally, we identify and implement a mechanism through which a single diffusion model can be applied to measurements obtained from multiple measurement operators. Taken together, the contents of this manuscript provide a new understanding and several new directions in the application of diffusion models to solving physics-based inverse problems.

Solution of Physics-based Bayesian Inverse Problems with Deep Generative Priors

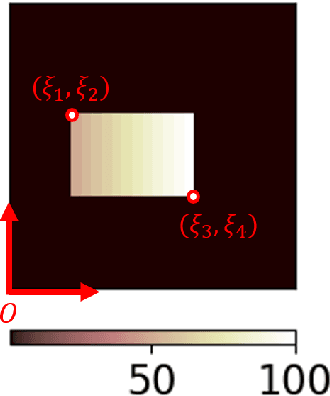
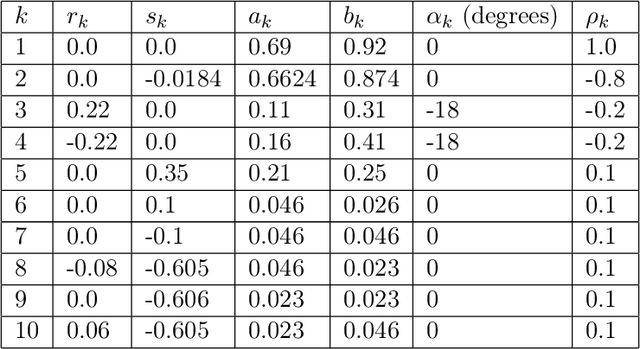
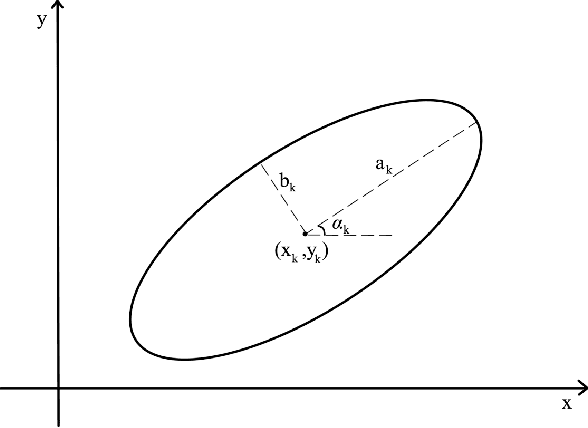
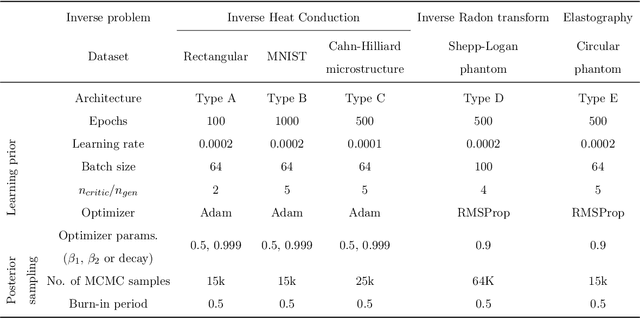
Inverse problems are notoriously difficult to solve because they can have no solutions, multiple solutions, or have solutions that vary significantly in response to small perturbations in measurements. Bayesian inference, which poses an inverse problem as a stochastic inference problem, addresses these difficulties and provides quantitative estimates of the inferred field and the associated uncertainty. However, it is difficult to employ when inferring vectors of large dimensions, and/or when prior information is available through previously acquired samples. In this paper, we describe how deep generative adversarial networks can be used to represent the prior distribution in Bayesian inference and overcome these challenges. We apply these ideas to inverse problems that are diverse in terms of the governing physical principles, sources of prior knowledge, type of measurement, and the extent of available information about measurement noise. In each case we apply the proposed approach to infer the most likely solution and quantitative estimates of uncertainty.

Bayesian Inference with Generative Adversarial Network Priors

Bayesian inference is used extensively to infer and to quantify the uncertainty in a field of interest from a measurement of a related field when the two are linked by a physical model. Despite its many applications, Bayesian inference faces challenges when inferring fields that have discrete representations of large dimension, and/or have prior distributions that are difficult to represent mathematically. In this manuscript we consider the use of Generative Adversarial Networks (GANs) in addressing these challenges. A GAN is a type of deep neural network equipped with the ability to learn the distribution implied by multiple samples of a given field. Once trained on these samples, the generator component of a GAN maps the iid components of a low-dimensional latent vector to an approximation of the distribution of the field of interest. In this work we demonstrate how this approximate distribution may be used as a prior in a Bayesian update, and how it addresses the challenges associated with characterizing complex prior distributions and the large dimension of the inferred field. We demonstrate the efficacy of this approach by applying it to the problem of inferring and quantifying uncertainty in the initial temperature field in a heat conduction problem from a noisy measurement of the temperature at later time.