Acceleration-Based Control of Fixed-Wing UAVs for Guidance Applications

Acceleration-commanded guidance laws (e.g., proportional navigation) are attractive for high-level decision making, but their direct deployment on fixed-wing UAVs is challenging because accelerations are not directly actuated and must be realized through attitude and thrust under flight-envelope constraints. This paper presents an acceleration-level outer-loop control framework that converts commanded tangential and normal accelerations into executable body-rate and normalized thrust commands compatible with mainstream autopilots (e.g., PX4/APM). For the normal channel, we derive an engineering mapping from the desired normal acceleration to roll- and pitch-rate commands that regulate the direction and magnitude of the lift vector under small-angle assumptions. For the tangential channel, we introduce an energy-based formulation inspired by total energy control and identify an empirical thrust-energy acceleration relationship directly from flight data, avoiding explicit propulsion modeling or thrust bench calibration. We further discuss priority handling between normal and tangential accelerations under saturation and non-level maneuvers. Extensive real-flight experiments on a VTOL fixed-wing platform demonstrate accurate acceleration tracking and enable practical implementation of proportional navigation using only body-rate and normalized thrust interfaces.

Online Obstacle evasion with Space-Filling Curves

The paper presents a strategy for robotic exploration problems using Space-Filling curves (SFC). The region of interest is first tessellated, and the tiles/cells are connected using some SFC. A robot follows the SFC to explore the entire area. However, there could be obstacles that block the systematic movement of the robot. We overcome this problem by providing an evading technique that avoids the blocked tiles while ensuring all the free ones are visited at least once. The proposed strategy is online, implying that prior knowledge of the obstacles is not mandatory. It works for all SFCs, but for the sake of demonstration, we use Hilbert curve. We present the completeness of the algorithm and discuss its desirable properties with examples. We also address the non-uniform coverage problem using our strategy.

Online Evasive Strategy for Aerial Survey using Sierpinski curve

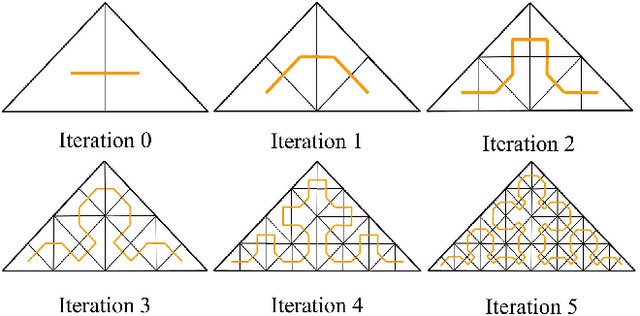
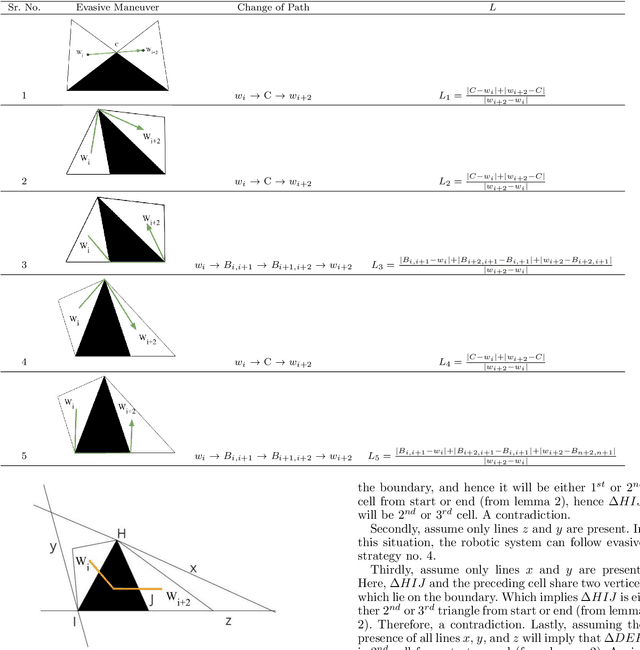
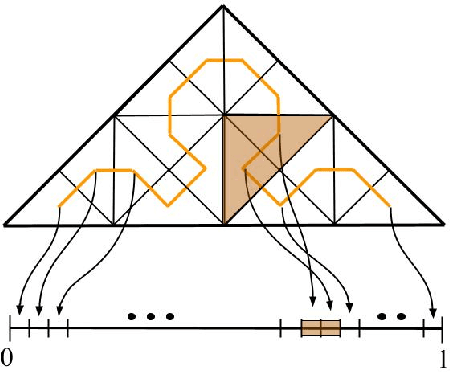
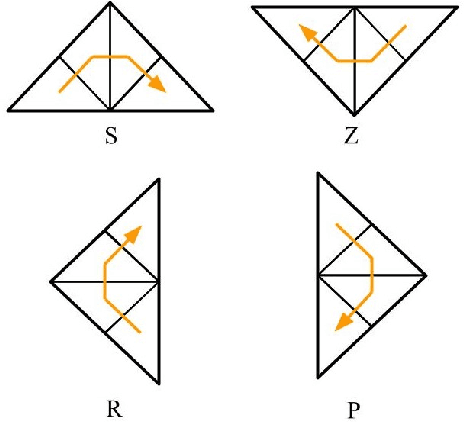
This paper deals with the aerial survey of a closed region using the Space-Filling curve, particularly Sierpinski curve. The specified region is triangulated, and the Sierpinski curve is used to explore each smaller triangular region. The entire region may have one or more obstacles. An algorithm is presented which suggests evasive manoeuvre (detour) if an obstacle is detected. The algorithm is online; that is, it does not require prior knowledge of the location of obstacles and can be applied while the robotic system is traversing the designated path. The fractal nature of the Sierpinski curve and simple geometric observations were used to formulate and validate the algorithm. The non-uniform coverage and multiple obstacle problems are also dealt with towards the end.