Constructing Extreme Learning Machines with zero Spectral Bias

The phenomena of Spectral Bias, where the higher frequency components of a function being learnt in a feedforward Artificial Neural Network (ANN) are seen to converge more slowly than the lower frequencies, is observed ubiquitously across ANNs. This has created technology challenges in fields where resolution of higher frequencies is crucial, like in Physics Informed Neural Networks (PINNs). Extreme Learning Machines (ELMs) that obviate an iterative solution process which provides the theoretical basis of Spectral Bias (SB), should in principle be free of the same. This work verifies the reliability of this assumption, and shows that it is incorrect. However, the structure of ELMs makes them naturally amenable to implementation of variants of Fourier Feature Embeddings, which have been shown to mitigate SB in ANNs. This approach is implemented and verified to completely eliminate SB, thus bringing into feasibility the application of ELMs for practical problems like PINNs where resolution of higher frequencies is essential.

Investigations on convergence behaviour of Physics Informed Neural Networks across spectral ranges and derivative orders

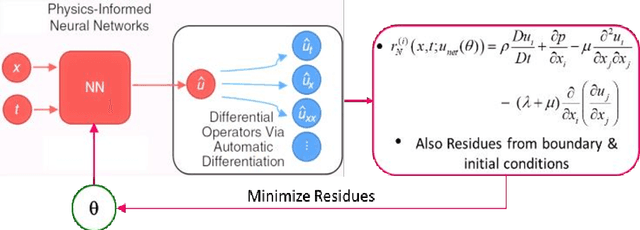
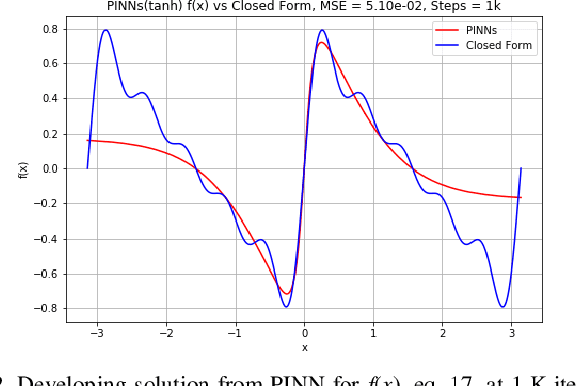
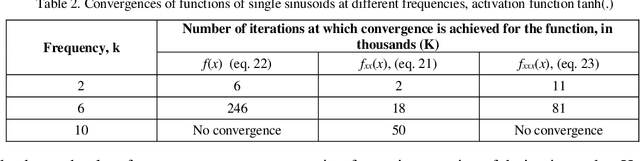
An important inference from Neural Tangent Kernel (NTK) theory is the existence of spectral bias (SB), that is, low frequency components of the target function of a fully connected Artificial Neural Network (ANN) being learnt significantly faster than the higher frequencies during training. This is established for Mean Square Error (MSE) loss functions with very low learning rate parameters. Physics Informed Neural Networks (PINNs) are designed to learn the solutions of differential equations (DE) of arbitrary orders; in PINNs the loss functions are obtained as the residues of the conservative form of the DEs and represent the degree of dissatisfaction of the equations. So there has been an open question whether (a) PINNs also exhibit SB and (b) if so, how does this bias vary across the orders of the DEs. In this work, a series of numerical experiments are conducted on simple sinusoidal functions of varying frequencies, compositions and equation orders to investigate these issues. It is firmly established that under normalized conditions, PINNs do exhibit strong spectral bias, and this increases with the order of the differential equation.