Investigations on convergence behaviour of Physics Informed Neural Networks across spectral ranges and derivative orders
Paper and Code
Jan 07, 2023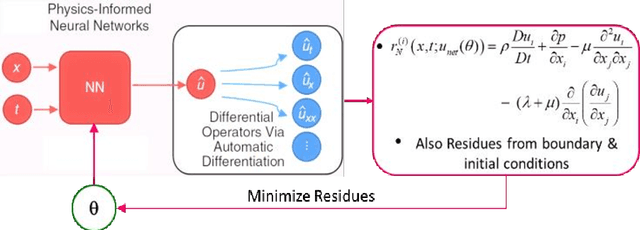

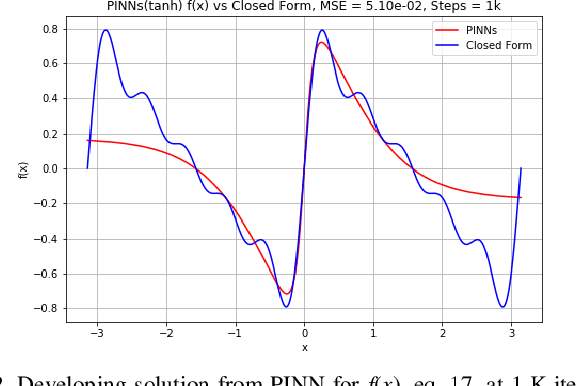
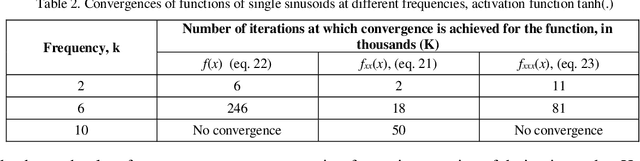
An important inference from Neural Tangent Kernel (NTK) theory is the existence of spectral bias (SB), that is, low frequency components of the target function of a fully connected Artificial Neural Network (ANN) being learnt significantly faster than the higher frequencies during training. This is established for Mean Square Error (MSE) loss functions with very low learning rate parameters. Physics Informed Neural Networks (PINNs) are designed to learn the solutions of differential equations (DE) of arbitrary orders; in PINNs the loss functions are obtained as the residues of the conservative form of the DEs and represent the degree of dissatisfaction of the equations. So there has been an open question whether (a) PINNs also exhibit SB and (b) if so, how does this bias vary across the orders of the DEs. In this work, a series of numerical experiments are conducted on simple sinusoidal functions of varying frequencies, compositions and equation orders to investigate these issues. It is firmly established that under normalized conditions, PINNs do exhibit strong spectral bias, and this increases with the order of the differential equation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge