Quantum-Inspired Edge Detection Algorithms Implementation using New Dynamic Visual Data Representation and Short-Length Convolution Computation

As the availability of imagery data continues to swell, so do the demands on transmission, storage and processing power. Processing requirements to handle this plethora of data is quickly outpacing the utility of conventional processing techniques. Transitioning to quantum processing and algorithms that offer promising efficiencies over conventional methods can address some of these issues. However, to make this transformation possible, fundamental issues of implementing real time Quantum algorithms must be overcome for crucial processes needed for intelligent analysis applications. For example, consider edge detection tasks which require time-consuming acquisition processes and are further hindered by the complexity of the devices used thus limiting feasibility for implementation in real-time applications. Convolution is another example of an operation that is essential for signal and image processing applications, where the mathematical operations consist of an intelligent mixture of multiplication and addition that require considerable computational resources. This paper studies a new paired transform-based quantum representation and computation of one-dimensional and 2-D signals convolutions and gradients. A new visual data representation is defined to simplify convolution calculations making it feasible to parallelize convolution and gradient operations for more efficient performance. The new data representation is demonstrated on multiple illustrative examples for quantum edge detection, gradients, and convolution. Furthermore, the efficiency of the proposed approach is shown on real-world images.

An Efficient Calculation of Quaternion Correlation of Signals and Color Images

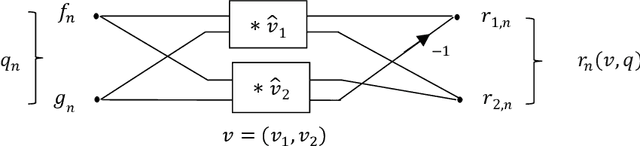
Over the past century, a correlation has been an essential mathematical technique utilized in engineering sciences, including practically every signal/image processing field. This paper describes an effective method of calculating the correlation function of signals and color images in quaternion algebra. We propose using the quaternions with a commutative multiplication operation and defining the corresponding correlation function in this arithmetic. The correlation between quaternion signals and images can be calculated by multiplying two quaternion DFTs of signals and images. The complexity of the correlation of color images is three times higher than in complex algebra.

Color-Coded Symbology and New Computer Vision Tool to Predict the Historical Color Pallets of the Renaissance Oil Artworks

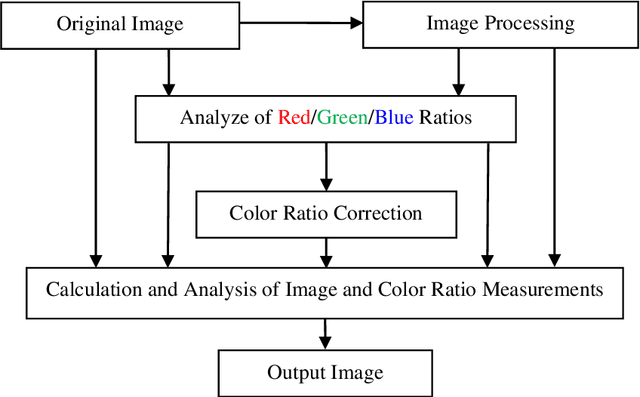
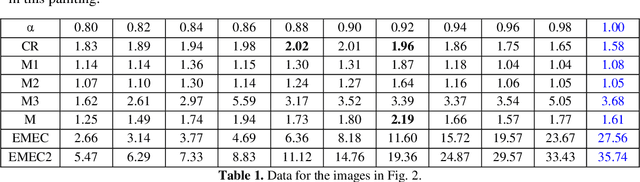
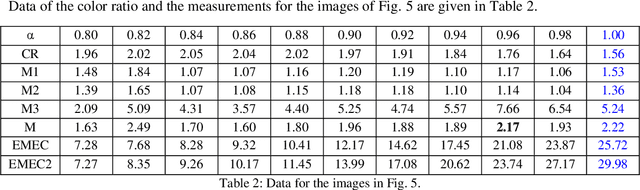
In this paper, we discuss possible color palletes, prediction and analysis of originality of the colors that Artists used on the Renaissance oil paintings. This framework goal is to help to use the color symbology and image enhancement tools, to predict the historical color palletes of the Renaissance oil artworks. This work is only the start of a development to explore the possibilities of prediction of color palletes of the Renaissance oil artworks. We believe that framework might be very useful in the prediction of color palletes of the Renaissance oil artworks and other artworks. The images in number 105 have been taken from the paintings of three well-known artists, Rafael, Leonardo Da Vinci, and Rembrandt that are available in the Olga's Gallery. Images are processed in the frequency domain to enhance a quality of images and ratios of primary colors are calculated and analyzed by using new measurements of color-ratios.

Alpha-rooting color image enhancement method by two-side 2-D quaternion discrete Fourier transform followed by spatial transformation

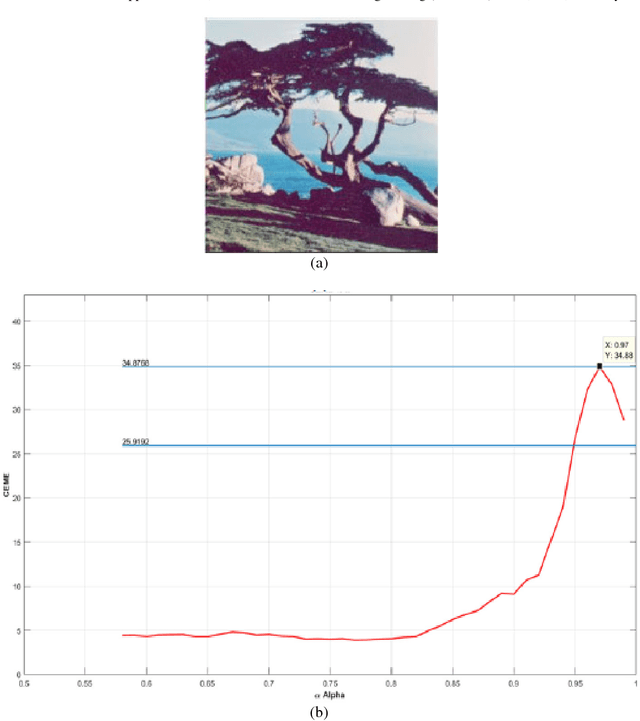
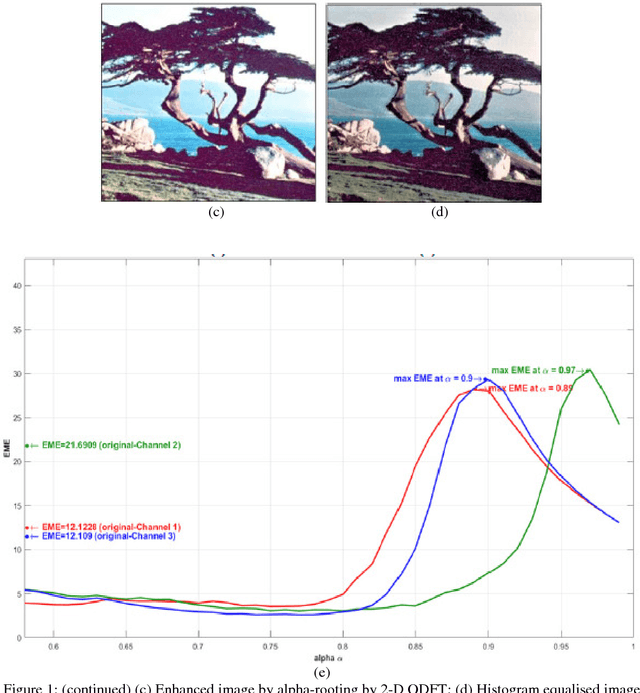
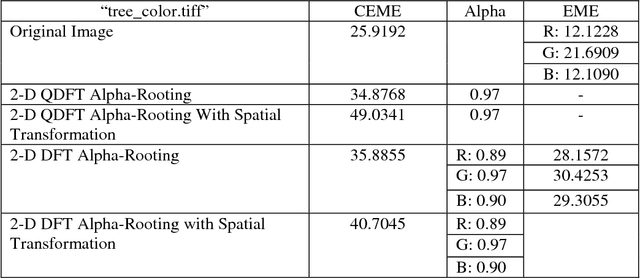
In this paper a quaternion approach of enhancement method is proposed in which color in the image is considered as a single entity. This new method is referred as the alpha-rooting method of color image enhancement by the two-dimensional quaternion discrete Fourier transform (2-D QDFT) followed by a spatial transformation. The results of the proposed color image enhancement method are compared with its counterpart channel-by-channel enhancement algorithm by the 2-D DFT. The image enhancements are quantified to the enhancement measure that is based on visual perception referred as the color enhancement measure estimation (CEME). The preliminary experiment results show that the quaternion approach of image enhancement is an effective color image enhancement technique.

Modified Alpha-Rooting Color Image Enhancement Method On The Two-Side 2-D Quaternion Discrete Fourier Transform And The 2-D Discrete Fourier Transform

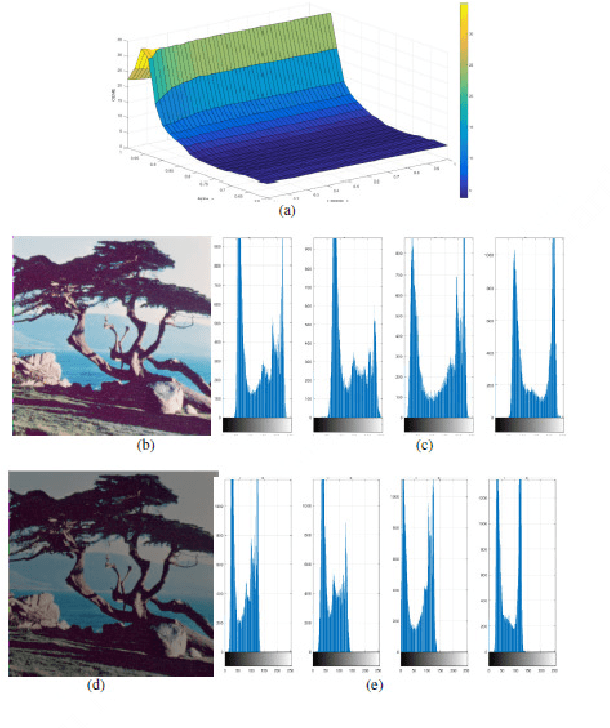
Color in an image is resolved into 3 or 4 color components and 2-Dimages of these components are stored in separate channels. Most of the color image enhancement algorithms are applied channel-by-channel on each image. But such a system of color image processing is not processing the original color. When a color image is represented as a quaternion image, processing is done in original colors. This paper proposes an implementation of the quaternion approach of enhancement algorithm for enhancing color images and is referred as the modified alpha-rooting by the two-dimensional quaternion discrete Fourier transform (2-D QDFT). Enhancement results of this proposed method are compared with the channel-by-channel image enhancement by the 2-D DFT. Enhancements in color images are quantitatively measured by the color enhancement measure estimation (CEME), which allows for selecting optimum parameters for processing by the genetic algorithm. Enhancement of color images by the quaternion based method allows for obtaining images which are closer to the genuine representation of the real original color.