Arthur Kramer
Exact and heuristic methods for the discrete parallel machine scheduling location problem
Jun 09, 2020



Abstract:The discrete parallel machine makespan scheduling location (ScheLoc) problem is an integrated combinatorial optimization problem that combines facility location and job scheduling. The problem consists in choosing the locations of $p$ machines among a finite set of candidates and scheduling a set of jobs on these machines, aiming to minimize the makespan. Depending on the machine location, the jobs may have different release dates, and thus the location decisions have a direct impact on the scheduling decisions. To solve the problem, it is proposed a new arc-flow formulation, a column generation and three heuristic procedures that are evaluated through extensive computational experiments. By embedding the proposed procedures into a framework algorithm, we are able to find proven optimal solutions for all benchmark instances from the related literature and to obtain small percentage gaps for a new set of challenging instances.
A unified heuristic and an annotated bibliography for a large class of earliness-tardiness scheduling problems
Jan 10, 2017
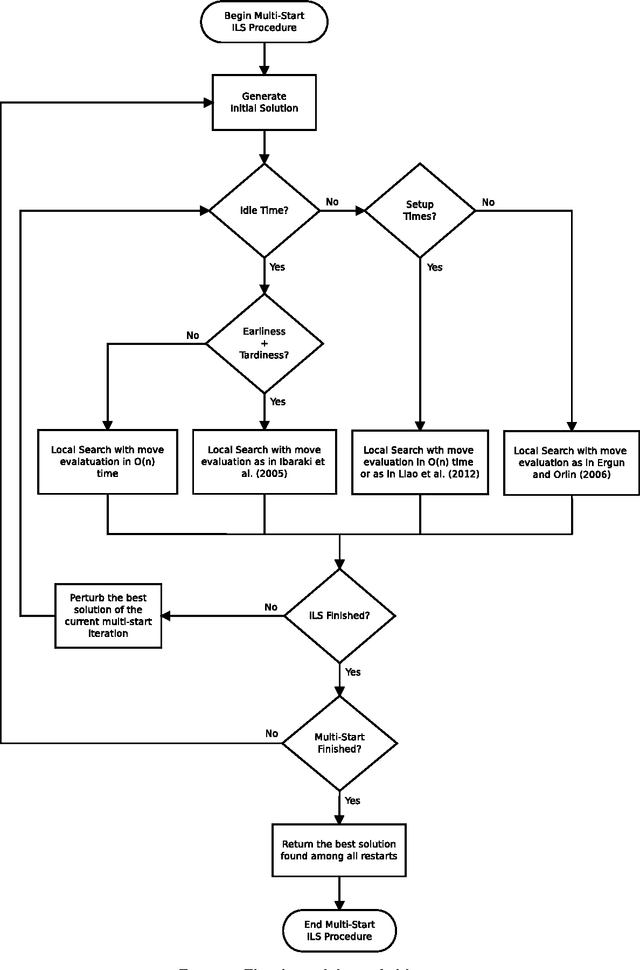
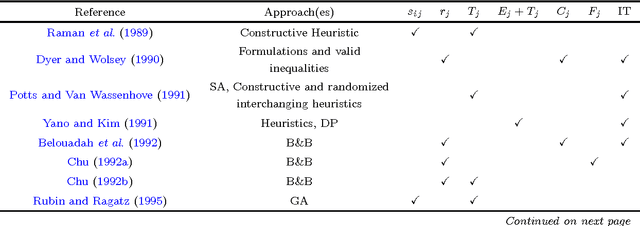

Abstract:This work proposes a unified heuristic algorithm for a large class of earliness-tardiness (E-T) scheduling problems. We consider single/parallel machine E-T problems that may or may not consider some additional features such as idle time, setup times and release dates. In addition, we also consider those problems whose objective is to minimize either the total (average) weighted completion time or the total (average) weighted flow time, which arise as particular cases when the due dates of all jobs are either set to zero or to their associated release dates, respectively. The developed local search based metaheuristic framework is quite simple, but at the same time relies on sophisticated procedures for efficiently performing local search according to the characteristics of the problem. We present efficient move evaluation approaches for some parallel machine problems that generalize the existing ones for single machine problems. The algorithm was tested in hundreds of instances of several E-T problems and particular cases. The results obtained show that our unified heuristic is capable of producing high quality solutions when compared to the best ones available in the literature that were obtained by specific methods. Moreover, we provide an extensive annotated bibliography on the problems related to those considered in this work, where we not only indicate the approach(es) used in each publication, but we also point out the characteristics of the problem(s) considered. Beyond that, we classify the existing methods in different categories so as to have a better idea of the popularity of each type of solution procedure.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge